34 Minuten
“Generative Audio Synthesis” refers to a process in which computers assist in sound design and the calculation of sonic structures. These processes can range from being fully automated to allowing significant control by the composer, balancing between algorithmic autonomy and creative direction.
In the 20th century, the contemporary music landscape began to blur the lines between composing the sound itself and composing with sound. The composition of timbre became a structural element. This evolution emerged from gaining access to sound design by handling recorded materials—such as the organization of multiple layers of sonic elements through the montage of tape reels. Starting with manual operations in studios like WDR (Westdeutscher Rundfunk) and GRM (Groupe de Recherches Musicales), then the introduction of computer hardware and software tools exponentially expanded the possibilities for both synthesizing sound and using it as a material for composition. There hasn’t been one path, one goal. The study of composing the sound and composition with the sound has broadened the possibilities among different schools, aesthetics, and techniques from post-war serialism to ambient sound design.
I am Sinan Bokesoy. I began my studies in electronic music at the Centre de Création Musicale Iannis Xenakis in Paris and completed my Ph.D. at the University of Paris under the guidance of Horacio Vaggione, focusing on self-evolving sonic structures. Over the past 25 years, I have dedicated myself to exploring algorithmic approaches in composition and sound design and developing professional audio applications through sonicLAB/sonicPlanet, entities I founded. My aim has always been to establish a balanced workflow that bridges theory and practice, as well as artistic and scientific approaches.
Generative audio encompasses multiple disciplines: the science of sound, mathematics, physics, compositional theories, and the knowledge and practical experience of applying them as an artist. Even focusing on a small part of this vast domain can require a lifetime of research and creation to yield rigorous results. This is especially true in the continuous evaluation, refinement, and reiteration of ideas and theories, which is a core activity in my development process. I approach this article from neither a purely academic level nor a beginner’s perspective, but rather somewhere in between, suited for those with a foundational understanding seeking deeper insight.
The Concept of “Generative”
How do cold calculations transform into captivating soundscapes or organized musical forms?
Generative processes in music, the concept of using procedures of translating information for creative purposes, have existed for centuries. For example, Guido d’Arezzo ( 990 - 1033 ) developed a model by mapping vowels from text to specific pitches (Figure 1), creating melodic phrases that honored the meaning of the words being sung. The translation of the phonemic structure of a text to pitches of a plainsong with the following mapping:
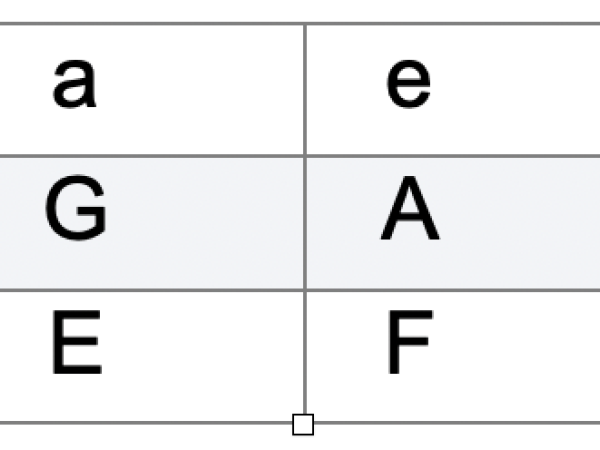
Figure 1. Mapping of vowels to pitch values.
This is an early example of how structured rules can be applied to generate musical mapping. Who can deny that the fugue technique, in the hands of J.S. Bach (1685-1750), is a remarkable example of a compositional generative model? It assisted in crafting some of the finest art in music, providing a structured framework for the vertical and horizontal organization of musical ideas, a type of multi-dimensional mapping for both creativity and complexity.
Coming back to our century, in computer-assisted sound design and composition, “generative” describes a creative approach where music or sound elements are algorithmically produced, with minimal human intervention beyond setting the initial parameters or rules. This method relies on systems that can autonomously generate or evolve content through algorithms, often focusing on specific structures and needs—such as controlled randomness, procedural rules, models of physical processes, variation of machine-learned models ( Generative AI ), computational techniques that exploit the computer’s strength in number crunching.
By utilizing these generative processes, composers and sound designers can explore sonic textures, patterns, and structures that might be unattainable through manual methods.
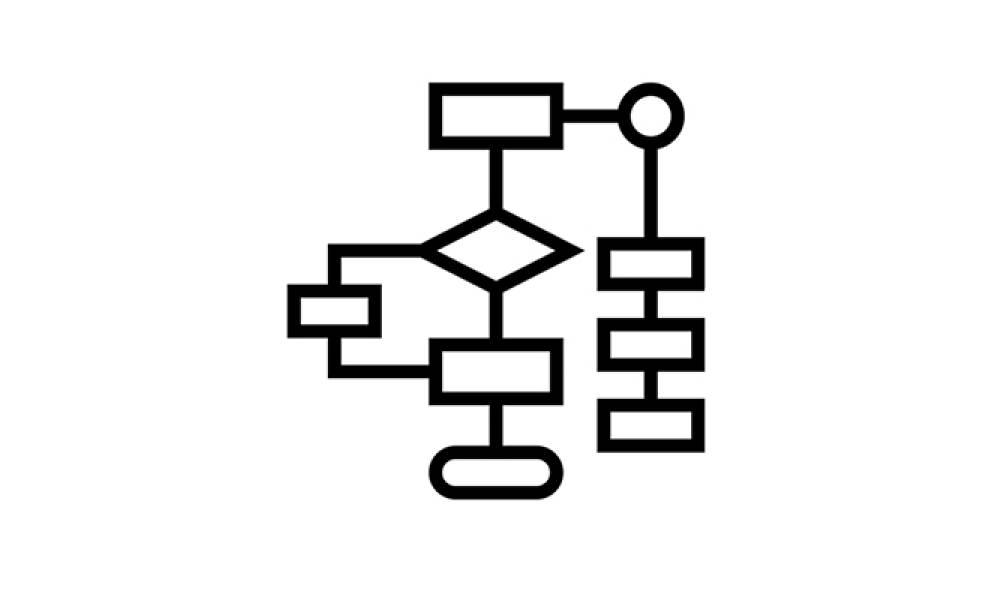
Algorithms serve as goal-oriented recipes, combining functional blocks to accomplish specific tasks. The flow diagram of computer software is naturally structured the same way, there is a start and then end, the input and the output. (Figure 2) How to fill in these blocks depends on the purpose.
Although the algorithms can be quite simple in structure, they can also yield complex outputs, mirroring many procedural or evolutionary processes found in nature. However, it’s important to distinguish Generative AI from these algorithms due to its immense complexity and opaque nature. There are multiple steps in creating a machine learning model with preparation of training data, training process, and evaluation of the model which cannot be described by blocks of operations as above.
The most beautiful and intricate art often arises from simple foundational ideas, much like evolutionary processes in nature. Evolution demonstrates how complexity can emerge from straightforward principles — such as variation, selection, and replication — applied over time and on multiple scales ( fractal structures ). Applying this concept to the realm of algorithmic composition and generative music suggests that the underlying algorithms and mathematical principles can often be distilled into a series of simple but effective steps. The elegance of this approach lies in avoiding unnecessary complexity within the algorithm’s structure itself, allowing richness and depth to emerge from the interaction of these simple rules over time. Too much complexity destroys itself and it is a virtue to avoid this in algorithmic design.
Pre-Computer Methods
From Edgar Varese, Luigi Russolo to Pierre Schaeffer, the motivation for using new sounds was to find a breach in the fortress of musical tradition, each creation through a personal manifesto. The motivation to create the tools to assist in sound design and not invent a machine that can do the compositional task in place of the composer.
As György Ligeti once noted, “A computer will not create a composition on its own; it is the interaction between the composer and the computer that creates the composition.” In the context of today’s technology, we can indeed build complex and autonomous systems, but the generative process should still ideally function as an instrument with which the composer interacts, rather than as a monolithic, self-contained system.
Reflecting on our recent past, there was a time when digital means for recording audio were virtually nonexistent. Composers experimented with electronic sound through manual operations, such as chopping tape recordings of sound (concrete material) in analog environments to construct multiple layers with polyrhythmic structures, vertical and horizontal complexities, and evolving timbral textures. Tone generators were used to create post-serial clusters and to abstract sound from its source, merging different contexts.

Figure 3. Pre-DSP age electronic music labs.
Until then, the music creation process had no plastic qualities – composers conceived music, then wrote marks on paper that corresponded to the stable frequencies of musical notes, intended for performance. Prepared and composed music with tape recording tools, on the other hand, could not pre-exist, but was a product of its constituent recorded elements. Similar to the toolset of a carpenter/sculptor, shaping the creation by manipulating the material through physical processes, these electronic music laboratories (Figure 3) provided the first environments where composers could reshape the sonic material and create their compositional form.
This layering and processing of sonic material allowed for an exploration of sonic emergence, offering invaluable experience in creating timbral compositions that extend beyond traditional orchestral sounds. Ligeti himself acknowledged that his work at the WDR electronic music studios was essential in developing the techniques used in his piece Atmosphères (1961), particularly in generating dense tone clusters. The static character of electronic music is reflected in the sonic texture of Atmosphères, where the vertical layering of sound materials on a micro-scale enabled continuous control over the spectra-morphology of sound. Numerous independent musical lines (micro-polyphonie) blended and blurred their boundaries and this style became a hallmark of Ligeti. The reason I do mention his work Atmosphères is the gradual transformation of sound masses, evolving that moves organically like in gases, allowing for subtle shifts in texture and color. Figure 4, illustrates the mass movement and dynamic structure of Atmosphères’ sonic texture, clearly showing how it evolves within the pitch boundaries.
How to create algorithmic models shaping the musical structure on multiple dimensions?
Timbre as a structure has multiple dimensions, pitch, and intensity being only the emergent outcomes. The challenge is to create multiple layers of sonic material, shaping both the horizontal and vertical structure of timbral composition as if it were an instrument—an intelligent composition of time and perceptual information that engages our auditory system.
Again, the algorithmic approach to sound creation in the 20th century was not about programming computers to create variations of Bach or Debussy. Instead, it was about advancing sound composition by handling vast amounts of information on a microscopic level, studying the spectral structure of sound, and integrating these findings into compositions that include both electronic and acoustic elements. It involves dealing with sound beyond traditional notation, using abstract values and multimodal representations.
My explorations of these issues are rooted in the academic path I have chosen. My interaction with electronic music began through the works of Iannis Xenakis at the Centre de Création Musicale Iannis Xenakis while studying composition in Paris.
Inspired by scientific advancements in physics and astronomy, composers look to natural processes as sources of inspiration. Randomness is foundational to the universe, from quantum events to the organization of large particle structures. The science of statistics was developed to understand, control, simulate, and predict these structures. The constant flux of natural processes is a fertile ground for developing sonic morphology and timbral movement as elements of a continuous composition. Aleatoric, or random processes in music have long been a focus of avant-garde composers exploring the boundaries of unpredictability.
For instance, John Cage’s use of randomness, as inspired by the I-Ching (an ancient Chinese divination text), reflects his philosophy of removing personal bias from the compositional process. By employing chance operations like flipping a coin or rolling dice to determine elements such as pitches, rhythms, or dynamics, Cage sought to democratize the compositional process, allowing all possibilities an equal chance to manifest. This approach aligns with his interest in Zen Buddhism, emphasizing acceptance, openness, and the absence of preconceptions.
Cage’s works like “Music of Changes” and “4’33” highlight his commitment to unpredictability and the inclusion of all sounds—whether traditionally musical or environmental—as part of a composition. As Heraclitus observed, “You cannot step into the same river twice.”
Iannis Xenakis’ Pioneering Algorithmic and Mathematical Approaches
Iannis Xenakis took a unique and radical approach to composition, merging his expertise in music, architecture, and mathematics to pioneer generative and algorithmic processes. Even without the initial aid of digital computers, Xenakis employed mathematical methods, such as stochastic processes, set theory, and game theory, to formalize his music. His algorithms, crafted through analog calculations, aimed to break free from traditional forms and conventions. In his manifesto, Xenakis envisioned liberating every component of sound and musical composition from past paradigms. For him, this meant stripping away predefined structures and rules to reach a pure form of creativity grounded in mathematical logic, scientific principles, and a profound engagement with the fundamental elements of sound and form. By minimizing constraints, he believed that artists could tap into a more primal understanding of music and art, reflecting natural processes and forces.
Xenakis championed the use of mathematical models, and probabilistic techniques to generate musical forms that are unpredictable yet governed by underlying scientific laws. This approach is not about eliminating rules entirely but rather choosing the simplest, most fundamental constraints that mirror the complexity of the natural world. Through this, Xenakis believed artists could create works that are more dynamic, organic, and in harmony with the forces and patterns of nature.
Xenakis translated mathematical data into tape manipulations and orchestration for acoustic instruments. His compositions are recognized for their intricate layers and the use of mathematical models to shape the density, dynamics, and evolution of sound masses over time. Furthermore, these techniques are quite transparent in his creations be it to create complex textures, or forms in pieces like “Metastasis”, or “Achorripsis”. Now I would like to introduce a breakdown of the mathematical concepts that form the basis of his compositions “Metastasis”, “Achorripsis” and “Concrete PH”.
“Metastasis (1953-54)”
“Metastasis” can be understood as “beyond immobility” or “change after stillness.” In the context of the composition, “Metastasis” refers to the gradual transformation of sound masses over time. In Metastasis, Xenakis utilized stochastic processes to structure the glissandi (continuous pitch slides) of string instruments. He applied statistical methods to control the density and dynamics of masses, which created a sense of randomness and unpredictability while adhering to an underlying probabilistic model. This approach mirrors the natural phenomena of complex systems, such as the patterns of bird flocks or crowd movements, where individual elements act seemingly at random (micro-scale) but collectively form coherent structures. ( macro-scale )
To control the movement of sound masses Xenakis utilized Gaussian (or normal) distributions (Figure 5). It allowed Xenakis to model the spread and convergence of sound events, resulting in evolving soundscapes that resemble natural processes like fluid dynamics or thermal diffusion.
The Gaussian distribution, also known as the normal distribution, is a statistical function characterized best by its bell-shaped curve that describes how a set of values is distributed around a central point, known as the mean (μ), symmetrically. Most of the values are clustered around the mean, and the probability of values further away from the mean decreases exponentially. It is one of the most important probability distributions in statistics due to its natural occurrence in many real-world phenomena. The formula is as follows:
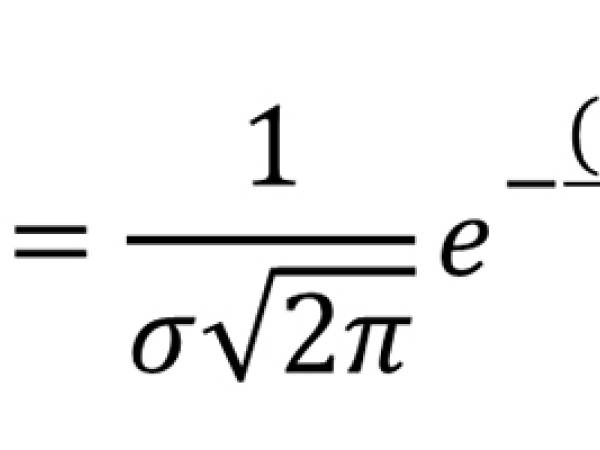
For its use on Metastasis, x represents a specific musical parameter (such as pitch or duration), μ is the mean (average value around which events cluster), and σ is the standard deviation (which determines the spread or concentration around the mean), was used to calculate the likelihood of certain musical events occurring at specific times or pitches. Xenakis adjusted these parameters (μ and σ) to shape the musical texture dynamically, deciding where the sound events would cluster more tightly or be more dispersed.
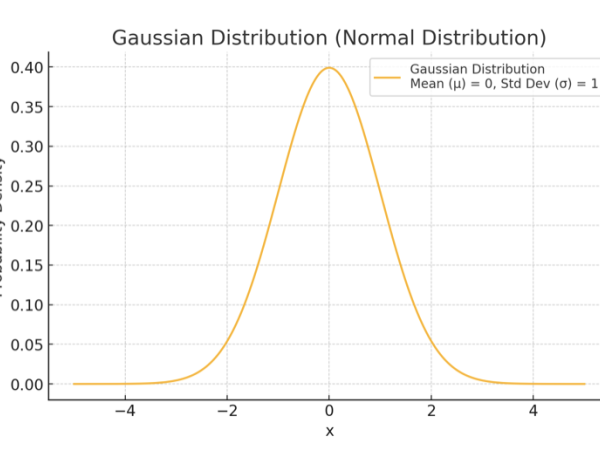
Figure 5. The bell-shaped distribution curve of events in Gaussian distribution.
Pitch and Glissandi: Xenakis is known for creating continuous pitch trajectories applied on string instruments. (Figure 6) The score of Metastasis depicts these movements as you can see in the figure above. Using Gaussian distributions to control the pitch and the density of glissandi (continuous slides between pitches) their distribution determined the starting and ending points of these glissandi, the rate of their movement, and their concentration within specific time frames. For example, pitches were distributed according to the bell curve of the Gaussian distribution, where most events cluster around a central pitch and fewer events occur at extremely high or low pitches. This created a texture where sound events are concentrated in the middle register and gradually dispersed toward the higher and lower ends, mimicking the spread of particles in a fluid.
Duration and Dynamics: The Gaussian distribution also influenced the duration and dynamics of sound events to create patterns where the duration of notes or sound masses is more frequent around a central value, with shorter or longer durations becoming progressively less common. Similarly, the dynamic levels (loudness) of these events could be shaped so that most sounds cluster around a medium intensity, with fewer sounds at very soft or very loud levels. This probabilistic shaping gave the piece a sense of organic flow, where density and intensity evolved naturally over time.
Density of Sound Events: In Xenakis’s context, “density” refers to the number of sound events occurring within a given time span and the spatial distribution of these events across the pitch spectrum. Gaussian distribution helped determine how tightly or loosely packed these events were at any moment.

Figure 6. “Metastasis” score bars 317-333. Source: Iannis Xenakis, Musique, Architecture, Tournai, Castermann. 1976 p.8
For example, during climactic sections, the distribution would yield a high density of sound events clustered together, creating a thick, textured sound mass. In contrast, in quieter or less dense sections, the distribution would spread the events more sparsely, creating a sense of space and openness. This method allowed Xenakis to model sound masses in a way that resembles the behavior of particles under various forces, resulting in evolving soundscapes with fluid-like dynamics.
Xenakis’s background in architecture, particularly his collaboration with Le Corbusier on the Philips Pavilion, influenced the structural design of Metastasis. The work’s score ( see a sample shot above ) includes graphic notation that resembles architectural blueprints, using hyperbolic paraboloids—a shape used in the Pavilion’s design. Xenakis applied these geometric concepts to control the pitch and dynamic trajectories of musical events, treating them as architectural structures that develop over time.

Figure 7. Comparing the architecture of Phillips Pavilion and the score of Metastasis.
Concrete PH (1958)
Concrete PH (1958) is one of Iannis Xenakis’s pioneering works in electronic music. It is an example of musique concrète, where the sound material consists entirely of manipulated recordings using innovative techniques of sound manipulation.
Granular Synthesis Precursor: Concrete PH is recognized as one of the first pieces to exhibit a sonic texture akin to granular synthesis, predating both the terminology and the digital technology typically associated with it. Xenakis achieved this by meticulously editing and rearranging tiny segments of recorded sound from burning charcoal on magnetic tape ( Figure 8 ). The choice of burning charcoal was deliberate; it provided a natural sound source characterized by a chaotic pattern of crackles and pops, which inherently resembles a random distribution of events. This raw material served as an ideal candidate for Xenakis’s exploration of stochastic processes.
He deconstructed these recordings into small fragments, half seconds long, and manipulated their pitches and dynamics, resulting in a dense, textured sound mass that mimicked organic processes. This innovative approach utilized statistical methods and manual tape manipulation to create complex sound structures from simple elements.

Figure 8. Xenakis working in studio on Bohor, 1962.
Statistical Distributions and Manual Calculations: Xenakis used Poisson distributions to model the occurrence of these sound grains over time. The Poisson distribution is a probability distribution that describes the number of events occurring within a fixed interval of time or space when these events happen independently of each other and at a constant average rate. Unlike the Gaussian distribution, which is continuous, the Poisson distribution is discrete, meaning it deals with whole numbers (such as counts of events):
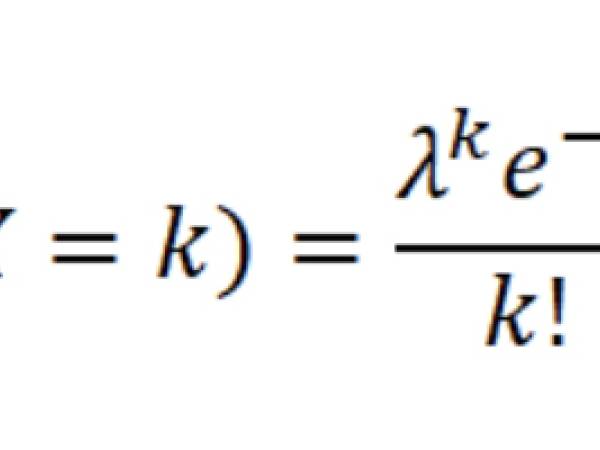
In a Poisson distribution (Figure 9), the mean (λ, lambda) represents both the expected number of occurrences (the average rate) and the variance (the spread of occurrences around the mean). This means that if the average rate of events is λ, the variance of the distribution is also λ.
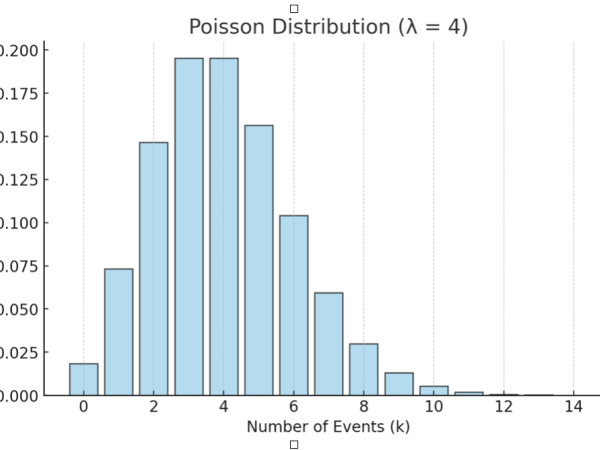
Figure 9. The Poisson distribution for discrete events.
The Poisson distribution is often used to model the number of events occurring within a fixed period or region, such as the number of phone calls received by a call center in an hour, the number of cars passing through a toll booth in a day, or even the number of sound events in a segment of a composition, as Xenakis did. This distribution was appropriate for modeling the random and sporadic nature of crackling charcoal, where individual sound events occur unpredictably over time. By applying the Poisson distribution, he controlled the density of the sound events—the number of sound grains occurring per unit of time—without imposing a fixed rhythmic structure. This allowed the sounds to appear randomly distributed, much like the pattern of raindrops hitting a surface or particles moving in a gas. (Figure 10)
Microsound and Sound Particles: In Concrete PH, Xenakis conceptualized sound in terms of “microsound” or tiny particles of sound. Each particle, or sound grain, was treated like a molecule in a gas, interacting with others according to stochastic rules. By applying stochastic distributions to both the time intervals and the parameters of the sound grains, Xenakis created a composition with multiple layers of complexity. The probabilistic approach allowed him to shape the density, duration, pitch, and dynamics of sound events in a way that closely mimics natural chaotic processes, such as fire crackling or water droplets. The result is a sonic texture that appears both random and coherent, as it follows the statistical patterns observed in nature.
Integration of Mathematical and Spatial Concepts: The title “PH” refers to the Philips Pavilion, designed by Xenakis and Le Corbusier for the 1958 Brussels World Expo, where the piece premiered. The composition was tailored to interact with the Pavilion’s distinctive acoustics and geometric structure, reflecting Xenakis’s interest in merging mathematical and physical models across different fields. The architecture’s unique shapes and surfaces influenced the diffusion of sound within the space, making Concrete PH an early example of spatialized sound design that integrates music with its physical environment.
Innovative Use of Tape Manipulation: In Concrete PH, Xenakis explored the possibilities of magnetic tape, the most advanced audio technology of his time. Xenakis meticulously calculated the probabilities and distributions to guide his manipulation of the magnetic tape. He manually cut, spliced, and varied the playback speeds of the tape fragments according to these calculations, thus implementing his stochastic methods with the technology available at the time. These analog techniques laid the foundation for future developments in electronic music, demonstrating how mathematical and statistical approaches could be applied to sound manipulation to create innovative textures and sonic forms.
Xenakis composed more orchestral works than electronic music pieces, primarily due to technological limitations at the time. The absence of personal computers and advanced programming environments made it challenging and labor-intensive to handle the vast amounts of data required for tape manipulation and sound synthesis. Additionally, the abstract numerical data generated through his calculations underwent a rigorous compositional process. Xenakis mapped these mathematical results to acoustic instruments, determining orchestration and defining the elements of the sonic texture, which led to the progressive development of his compositions. Therefore, the final work is not merely the output of an algorithm but the product of Xenakis’s creative process, where he designed the algorithmic framework and then integrated the results through a deliberate compositional strategy.
Xenakis has continuously extended his mathematical models and applied them in his tape music, orchestral music, and later his computer software developments to synthesize sound at the waveform level.
Achorripsis ( 1956 - 57 )
In Achorripsis, a creation for orchestral instruments, he has introduced the use of Markov chains to control transitions between consequent time frames, creating a form of narrative or evolution that is calculated for generating complex textures and structures that maintain coherence while embracing a high degree of variability.
His compositions Achorripsis, Analogique A, and B do simply showcase the use of all these models and are described in detail in his book “Formalized Music”.
Take a time frame of a certain length, like a bar. We would like to distribute some sonic events within this time frame. How many events? And when do they begin and end?
We can think about this as a top-down organization of events, starting with a time frame on a macro level and distributing the events in this space. Xenakis has chosen the Poisson probabilistic distribution to decide how many events should be in this space, for the reasons as explained above. Given a mean value, the Poisson formula distributes the density values around it.
For the onset and duration of events, Xenakis has used the exponential distribution, unlike the Poisson distribution, which is a continuous distribution. The Exponential distribution is a continuous probability distribution that is often used to model the time between independent events that occur at a constant average rate.
One of the key properties of the exponential distribution is its “memoryless” nature, meaning that the probability of an event occurring in the future is independent of any past events. The formula is the following and the distribution is in Figure 11.

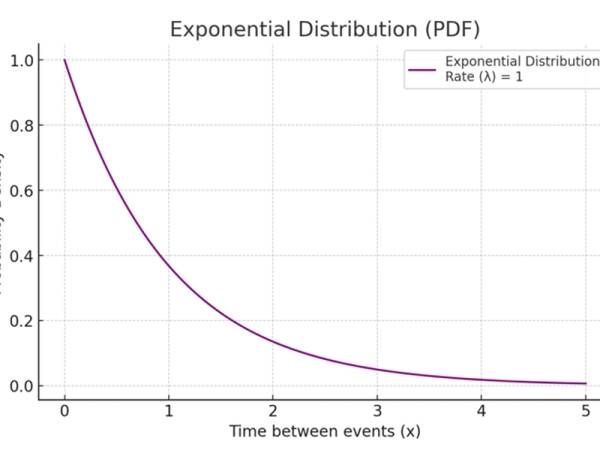
Figure 11. An example uses case of Exponential distribution modeling the probability versus the time between events.
In Figure 12, you can see an example distribution of events, where density is calculated with the Poisson distribution the onset/duration values with the Exponential distribution and the glissandi ramps with the Gaussian distribution.
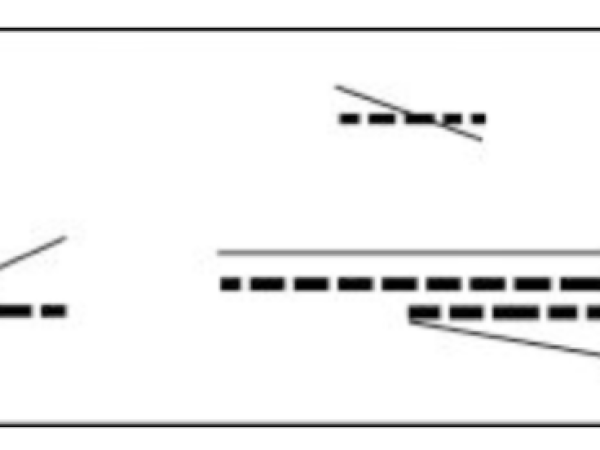
Figure 12. A time frame / cell with distributed events.
After this step, each distributed entity will gain an identity with parameters like pitch and intensity. According to Xenakis, a sonic entity has a multi-dimensional vector state in sonic space. Moving it from one point to another is a continuous operation at the micro level. (Figure 13) While individual events may be unpredictable on the micro-scale (like the roll of a single die), the overall behavior of a mass of events could be controlled and manipulated to achieve a desired musical effect on the macro scale. These are transitional gestures between order and total randomness/chaos.
Xenakis uses the Markov process to calculate a change in selected parameters among the sequence of frames. Markov process is a stochastic method where the probability of a future state depends only on the current state, not on the sequence of events that preceded it. This approach is particularly suited to modeling dynamic systems that evolve over time based on certain probabilities, which also establishes a level of interdependency between the event frames.
Xenakis divides Achorripsis into 28 distinct time/event frames or “sections.” Each section is characterized by different musical parameters such as pitch, dynamics, timbre, and density (the number of sound events). The transitions between these sections are governed by a Markov chain, which determines the likelihood of moving from one set of parameters to another. Here we use a matrix of probabilities that dictates which state (combination of musical parameters) will follow from the current state, ensuring a degree of unpredictability while still operating within a structured framework.
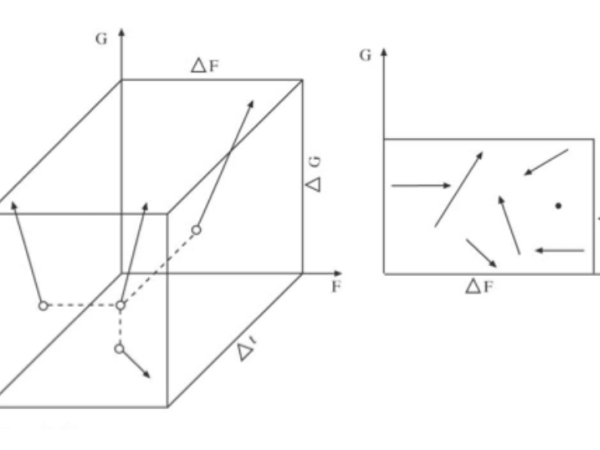
Figure 13. A sonic entity is defined as a vector with 3 dimensions.
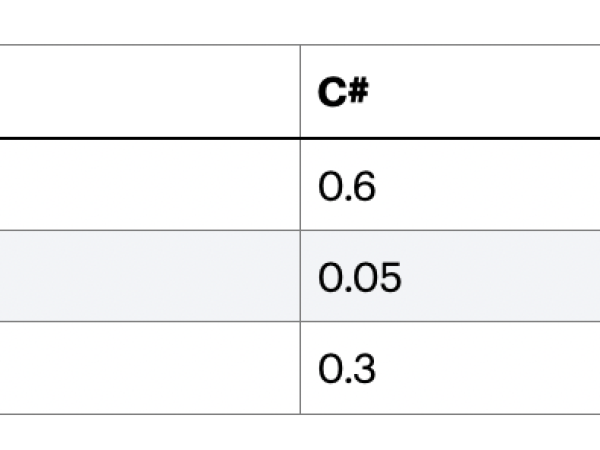
Figure 14. An example Markovian matrix defining transitions between pitch values.
Please note that the sum of each row must be 1, meaning that it is certain that one of these 3 choices will be chosen. We can read that a transition from note A to A has a probability of 10%, and from note A to C# has 60%. By looking at transitions C# to C# and Eb to Eb, we can say that this matrix does not give much chance that a note repeats itself. Just like modeling serial music partially!
In Figure 15, you can see the matrix of Achorripsis for the event density distribution among the instrument sections.
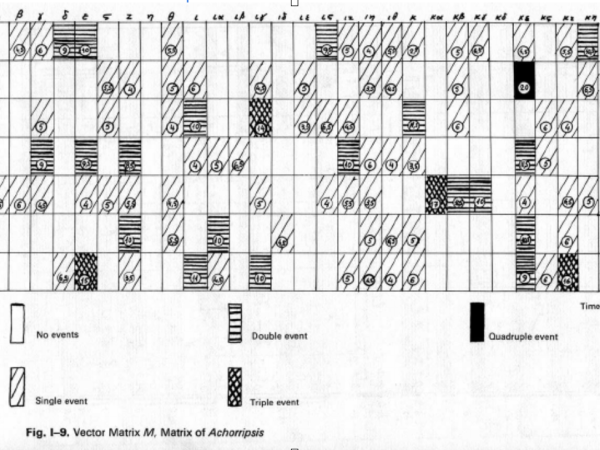
Figure 15. Xenakis description of Achorripsis density transitions over instrumental groups.
In Figure 16, Xenakis has noted the transition probabilities of frequency, intensity, and event densities applied each time frame.

Figure 16. Xenakis's description of frequency, intensity, and density transition matrices.
The Markovian process includes a special state known as the goal or absorbing state. Once the process reaches this state, it does not transition to any other state according to the normal rules; instead, it triggers a restart. When the Markov chain reaches the goal state, it “resets” to a starting state or a predefined set of initial conditions.
This restart can be deterministic (always returning to the same state) or probabilistic (choosing from a set of states based on an initial probability distribution). It is a point where the composer, such as Xenakis, can intervene in the generative process. After restarting, the Markov process begins again, following the same set of transition probabilities until it reaches the goal state once more.
This cycle repeats indefinitely or until a specific condition is met, allowing for different variations of recurring events. It also provides the composer with the flexibility to select a preferred transition process among multiple alternatives.
Xenakis outlined his compositional techniques in detail in his book “Formalized Music: Thought and Mathematics in Composition,” first published in 1971 by Indiana University Press, and republished in 1992 by Pendragon Press. In my view, this book serves as a foundational text for computer-assisted composition. Studying this comprehensive work during my student years allowed me to recreate these models and gain a deeper understanding of them.
My contributions
Compared to the technological tools available to Xenakis, I had access to a version of Max/MSP and an Apple PowerBook G4 in 2001. While studying his works, my aim was not to recreate his music but to use his models as a basis for developing structures that could be applied to sound synthesis techniques using contemporary digital audio tools. I recall creating a basic version of his GenDyn oscillator (stochastic waveform synthesis) in Csound, but soon after, I focused on his Achorripsis model. Developing such a complex event generation and modulation system in Max/MSP at that time was a programming challenge, especially since I wanted to maintain an interactive and real-time environment. Moreover, I lacked the skills to program a C++ application at that point.
The result was the creation of the “Stochos” application ( Figure 17 ), which garnered significant interest, was published academically, and led to the composition and performance of pieces at academic conferences. Applying these compositional models in real-time audio synthesis produced textures that would have been impossible to achieve through manual methods.
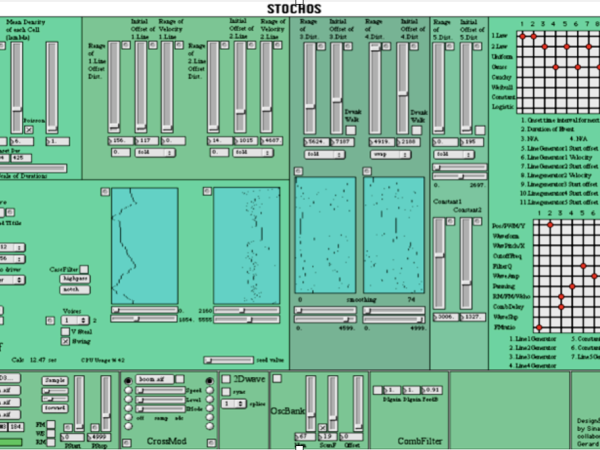
Figure 17. Stochos application developed on MaxMSP in 2001-2002.
Stochos did not incorporate a Markovian stochastic process to manage transitions between consecutive time frames, so there was no parameter dependency between frames. ( Figure 18 )However, it featured an event generation model that determined the density of events, their onset times, durations, and the length of each time frame using probabilistic distributions. Users could easily assign and experiment with different stochastic functions for each of these parameters.
Like Xenakis’s glissandi generators, Stochos included multiple ramp generators for each event based on stochastic calculations. These ramp generators could then be assigned to various synthesis operations, much like a matrix modulation interface on a synthesizer.

However, I quickly began to question how I could increase the complexity of the generative model to achieve sonic emergence across the micro, meso, and macro levels (vertical organization) while also establishing interdependencies in the progression. Inspired by natural processes, my solution was to apply self-similarity within complex structures, following a bottom-up approach akin to evolutionary development. I named this extended model “Cosmosf,” with the “f” representing feedback.
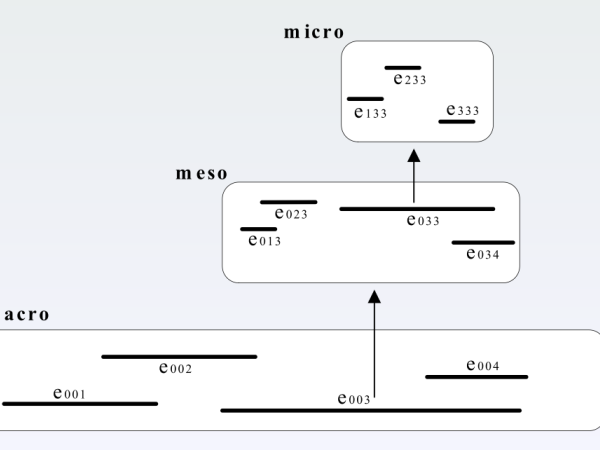
Figure 19. The Cosmosf model is a multi-scale and self-similar structure.
The Cosmosf model begins by opening a time frame on the macro scale and filling it with events, following the approach suggested by Xenakis. However, in this model, each event within the macro frame opens a new space on the meso scale, and each event within the meso frame opens another space on the micro-scale (Figure 19). This approach introduces self-similarity, enhancing complexity in vertical organization and creating new pathways for sonic emergence, much like processes found in nature.
In Xenakis’s model, the distributed events directly define the sonic entities, whereas in the Cosmosf model, this definition is carried by the micro-events. The meso events encompass the audio composition of each micro space, and the macro events encompass the audio composition of each meso space, resulting in a bottom-up organization.
Hierarchic structure — self-similarity — operations on multiple time scales
The realization of such a model in real-time audio software was possible thanks to the introduction of JavaScript support on MaxMSP in 2005. In Figure 20, you see the MaxMSP version assigning audio samples to each micro event.
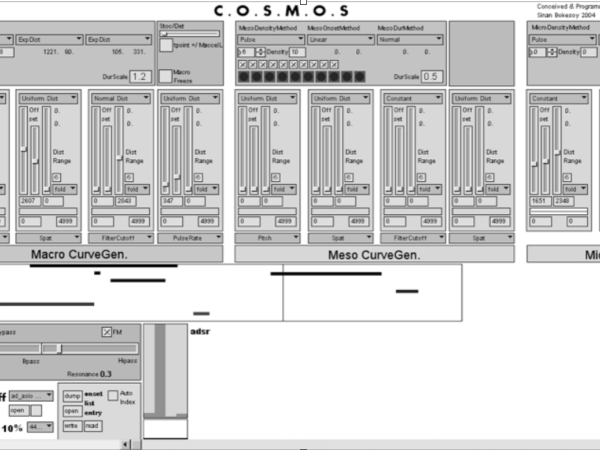
Figure 20. The Cosmosf model was realized first on MaxMSP in 2005 as a real-time event generator and synthesizer.
In 2006, I introduced a feedback loop from the macro scale output back to the micro-level sonic entities within the application. This means that the next macro time frame carries traces of the audio content from the previous macro output, which is then injected into the micro-scale of the new Cosmosf time frame.( Figure 21 )
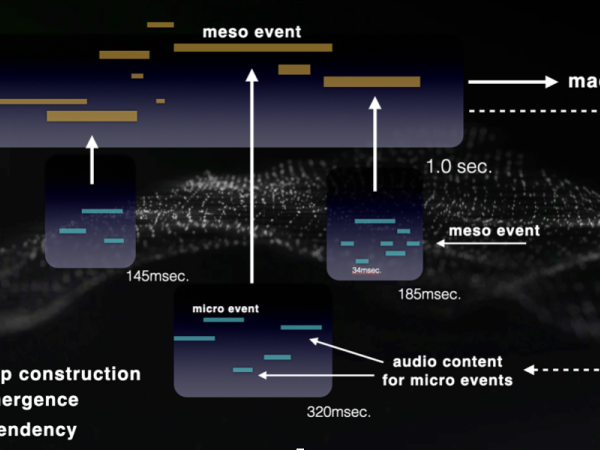
Figure 21. The bottom-up audio construction process with feedback.
In this model, the structure continuously updates its sonic content based on the output of the previous frame. The event generation remains top-down, while the audio construction is bottom-up, occurring across multiple time scales, much like emergent natural processes. The micro events are continuously influenced by the audio signals derived from the macro-level output.
Since Xenakis had no means of implementing such signal processing mechanisms, the output of his calculations was mapped directly to defined acoustic instruments. His approach relied on glissandi operations to shape the spectral density, rather than a bottom-up structure. It’s important to emphasize that the purpose of these applications is not to generate data for mapping to acoustic instruments alone. Instead, they offer the opportunity for these ideas and generative models to be applied across different genres of music.
Cosmosf software development: Saturn, FX and M31
I would say the development of Cosmosf truly began in 2011 after switching to a C++ API. This transition overcame many limitations, allowing me to push the CPU to its limits in favor of audio quality. The C++ version featured OpenGL graphics, a dedicated Tron-esque interface design, audio-rate calculations for every modulation source, and many custom DSP.
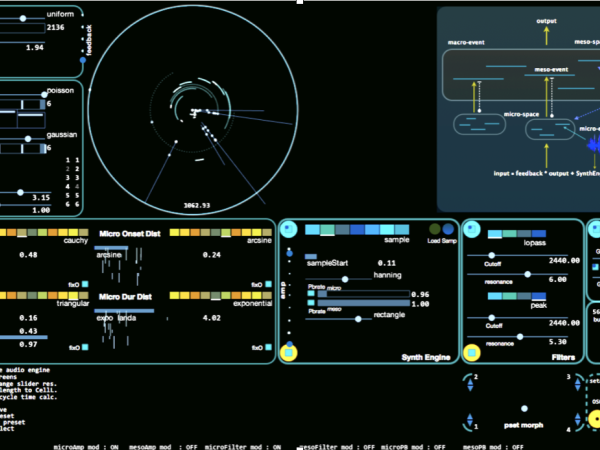
Figure 22. The first version of Cosmosf application was developed in C++.
The graphical capabilities of modern computers and the design for data visualization and interaction are subjects worth exploring in their own right—something that did not exist during Xenakis’s time. For Xenakis, data visualization was largely confined to score partitions.
A unique aspect of Cosmosf (2011) is its visualization of multi-scale and hierarchical event generation. Unlike the mono-scale event generation model, which uses a simple cell grid, Cosmosf represents the macro event as a full cycle. Within this cycle, arcs symbolize meso events, while dots indicate micro-events. (Figure 23)
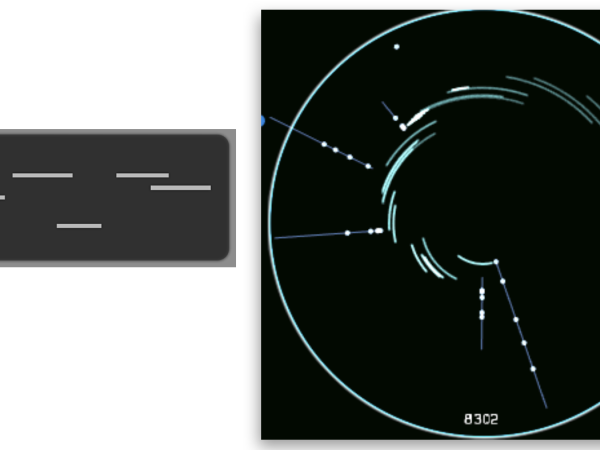
Figure 23. The visualization of multi-scale event distribution in Cosmosf.
Xenakis’s calculated glissandi model was initially implemented as LineGenerators in Stochos and later in Cosmosf. The line’s start offset and ramp speed can be modulated using a range of stochastic distributions available to the user.
Cosmosf also includes LFO (Low-Frequency Oscillator) generators, which can each be modulated by stochastic functions to vary their speed and amplitude/intensity parameters. As shown in Figure 24, this enables the creation of complex waveforms that function as modulation sources.
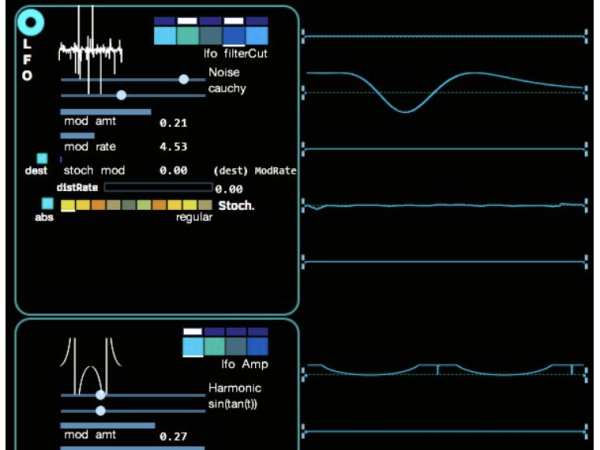
Figure 24. The stochastic LFO section on Cosmosf.
Each micro and meso event in Cosmosf is equipped with multiple LineGens and LFOs serving as modulation sources. The figure below illustrates the complexity that the application can achieve through its calculated data. You can also see a list of possible modulation destinations for both the LFO and LineGEN modulators. ( Figure 25 )

Figure 25. The modulation destinations of LFO’s and LineGen’s on Cosmosf.
To give you an idea of the computational potential of Cosmosf, here are some numbers: A single macro event can have up to 11 meso events, and each meso event can contain up to 11 micro-events. Each meso event includes 5 LineGens and 5 LFOs, while each micro-event has 6 LineGens and 5 LFOs. This structure demonstrates the application’s capacity for handling a significant amount of data and modulation sources, contributing to its complex and dynamic sound generation capabilities.
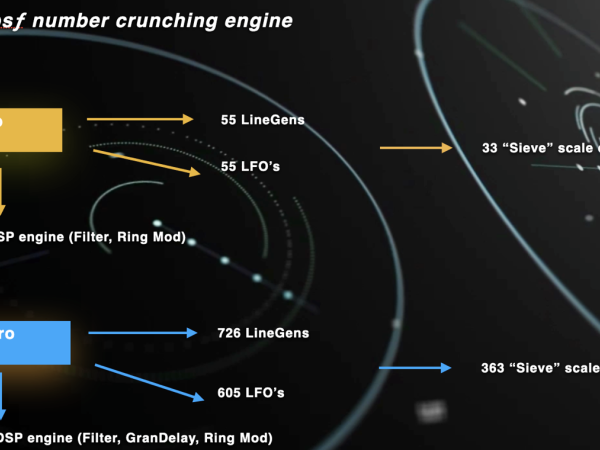
Figure 26. The calculation network in Cosmosf which increases in a fractal manner due to the multi-scale structure.
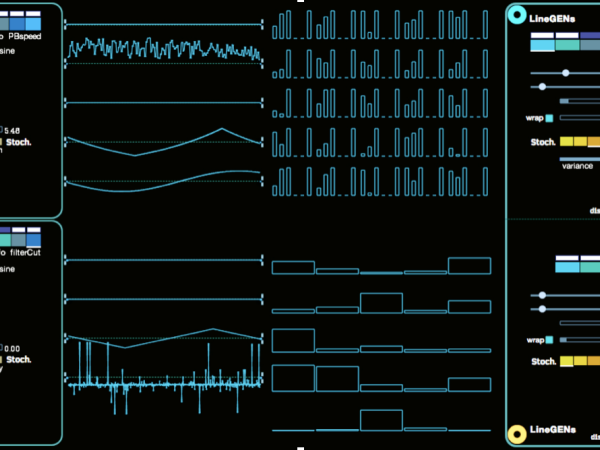
Figure 27. The modulation page projects all calculations in realtime.
Since Cosmosf v3, the event generation system includes dual macro events and two universes. The dual macro events can be thought of as para-phonic, while the two-universe system functions like parallel universes: the structure remains identical, but the outcomes differ because the iterations of the stochastic functions lead to different states. Figure 28 shows the systemic organization of both universes.
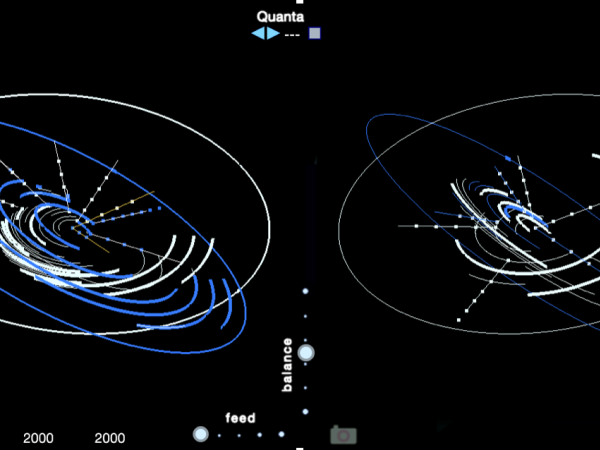
Figure 28. The dual universe and dual macro-event Cosmosf.
From one universe, the output of the macro sound can be fed to the second universe. These are inspirations of cosmological concepts applied to the Cosmosf model.
Operations on the calculated ( onset, duration ) event values :
Various operations can influence local density, the balance between total randomness and pattern loops, rhythmic quantization, and time compression or expansion. The left part of the application interface is dedicated to these time domain operations and can be accessed in real-time. ( Figure 29 )
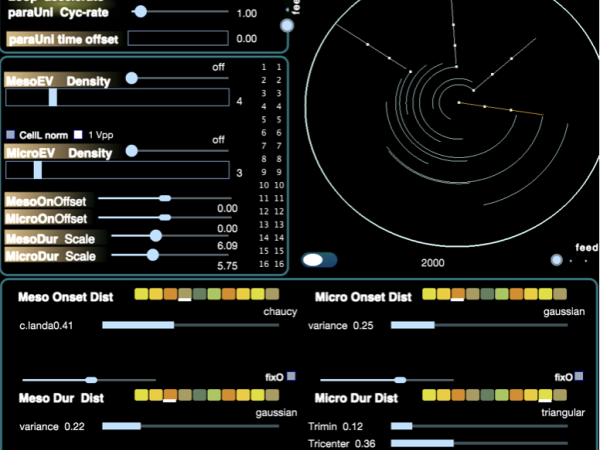
Figure 29. The event distribution parameters are concentrated on the left part.
- The results of stochastic distributions in Cosmosf can be quantized. Similar to a regular DAW sequencer, the onset and duration values of each micro and meso event can be aligned with classical note lengths, such as 4th, 8th, 16th, and 32nd, as well as triplet values. This allows the Cosmosf event generation system to function like a variation of an Euclidean sequencer, creating complex polyrhythmic structures.
- We can scale the durations of meso or micro events by a defined value, creating overlaps and thereby altering the local density.
- By continuously shrinking or expanding the arcs toward or away from the Cosmosf circle’s origin, we achieve time compression or expansion.
- Additionally, we can freeze the distributions for meso or micro events, causing the last calculated onset and duration values to remain fixed, resulting in a looping pattern at that scale.
Sieves
Cosmosf introduces one of the earliest uses of pitch quantizers, which take the raw values calculated by the modulators and quantize them to the selected musical scales or divisions. In Cosmosf, it is not only pitch but also other synthesis parameters that can be quantized at the meso or micro event level.
To visualize this process, I have associated the frequency spectrum with the color spectrum, aligning their respective wavelengths. This creates an intriguing correlation between the audible wavelengths of sound waves and the visible wavelengths of light waves. The upper part displays the raw values as a continuous line of the color spectrum, while the lower part shows the quantized states, represented as distinct dots. ( Figure 30 )
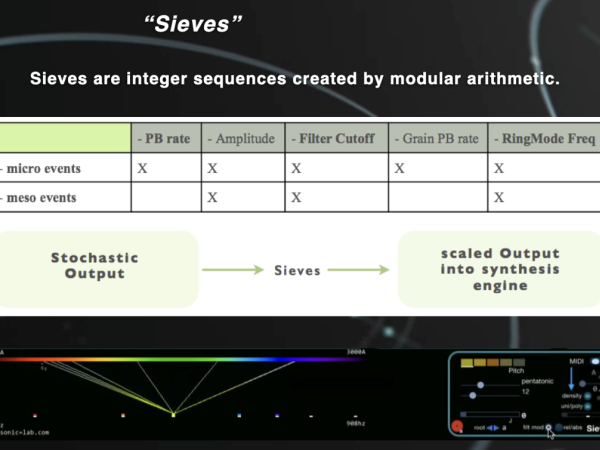
Figure 30. The Sieves interface represents sound frequencies with color wavelengths.
Morphing
A sonic morphing process defines a metaphor for exploring the sonic shape and timbral evolution on intermediate levels between two or more sonic materials. There is no robust methodology to bring exact solutions in morphing processes however they offer a rich terrain of possibilities that could be handled within various approaches to bring interesting perceptual phenomena.
Sound morphing can be performed by blending the parameters of the consistent structures that generate the source and destination sounds. An instance of the morphing process points to a certain state between two or more sounds/preset parameters which can be represented as a multi-dimensional vector in the parameter space.
In our case, this quantifiable and controllable sound entity is namely the one that is defined through the user interface / all the preset parameters that define the Cosmosf system that generates the sound. Hence each preset represents a vector state of pointing to an amount of parameters.
The morphing process in Cosmosf places four different presets at the corners of a tetrahedron, which touches the surface of a surrounding sphere. The morphing pointer represents any point within this sphere, and the Euclidean distance from this point to each preset determines the weight of that preset in the resulting parameter state. (Figure 31)
The morphing pointer can be moved manually by specifying polar coordinates within the sphere, using mathematical parametric functions (as shown in the figure on the left), or through controlled stochastic functions that adjust the polar coordinates (angles and radius).
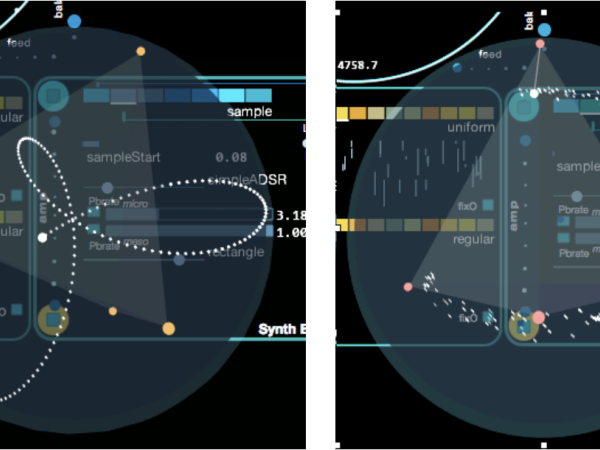
Figure 31. The Morphing pointer can be manipulated in various waves.
Introduced in 2013, the Cosmosf morphing engine was unique in its ability to perform the morphing process at an audio rate. This means that not only the individual morph states but also the behavior of the morphing pointer as it moves from point A to point B significantly influences the spectra morphology of the resulting sound.
3D sound spatialization in Cosmosf:
I have attended several important performances of Xenakis’s pieces, and one of the most striking aspects to witness live, with a full view of the entire scene (something often lost in recordings available on YouTube), is the interplay between the performers’ movements, the sound, and the space. In stochastic and chaotic processes, the iterative responses of individuals in crowd motion or flocking behavior vividly illustrate the emergent character of the system, where individual actions contribute to the collective dynamics. Xenakis utilizes this spatial distribution of events, making it visible in orchestral performances.
An event generation system like Cosmosf should be capable of conveying this movement through sound spatialization. Today, we can encode the source signal in ambisonic format, allowing each speaker in a projection system to contribute to the precise localization of the sound source within the performance space.
The late 2015 version of Cosmosf introduced the capability to render sound in a 3rd order ambisonic format and export it as a relevant multichannel audio file, which can be decoded later. The surround sound engine handles this by taking signals at the meso level and, similar to the 3D sphere used in the morphing engine, distributing their positions within this sphere.
Each meso event can be localized deterministically, moved along a curve using a parametric function, or positioned using controlled stochastic functions. (Figure 32)
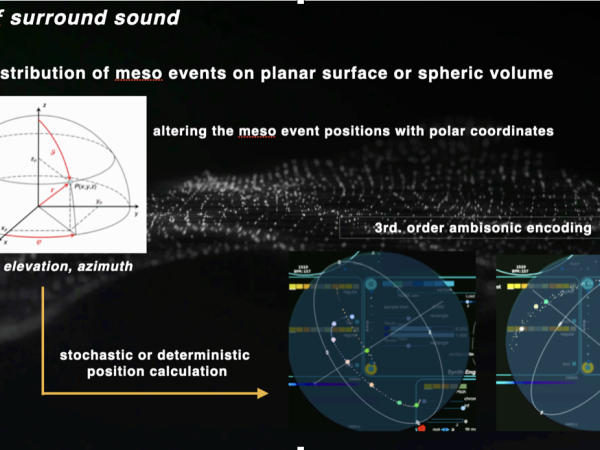
Figure 32. The sound spatialization process on meso events.
With this approach, by limiting the radius and polar angle parameters, events can be distributed within defined sections of the spatial field.
The availability of Cosmosf :
Cosmosf offers many additional features, but it is unnecessary to go into all the details here. I have highlighted the most notable innovative aspects and how Cosmosf diverges from Xenakis’s models. Currently, there are three versions available and distributed by www.sonic-lab.com : Cosmosf Saturn, Cosmosf FX, and Cosmosf M31. All come in the plugin format and run within a DAW.
Cosmosf Saturn is a synthesizer that generates micro-event audio content using assigned synthesis techniques, ranging from sample file playback to basic physical modeling.
Cosmosf FX is a live audio processor that focuses on the live audio processing capabilities of the Cosmosf synth engine. Structurally, both Cosmosf Saturn and Cosmosf FX are identical.
Cosmosf M31 is a MIDI event generator that creates MIDI note events for the micro and meso events of Cosmosf. These events include multiple LFOs and LineGens, which are translated into continuous MIDI controller messages. ( Figure 33 )

Figure 33. Cosmosf M31 and MBots running on a DAW.
Concluding the 1st Part of My Survey on Generative Audio Models
Generative audio synthesis and music continue to offer boundless opportunities for exploration, innovation, and development. To fully grasp their potential, it is essential to revisit and reinterpret old practices with new technological tools, engaging deeply with these processes to uncover their hidden dimensions. At its core, generative audio synthesis is not defined merely by the complexity of its models, algorithms, or AI, but by the depth with which these models can interpret, map, and evolve key sound design concepts, such as timbral development, sonic interaction, and structural intricacies. Its true essence lies in its ability to encapsulate and express the fundamental principles of sound composition, whether through simple or intricate systems and to reflect the unique vision and intent of its creator.
Throughout this survey, I have emphasized the historical foundations and central ideas behind generative models, exploring how they shape the composition of sound, both vertically and horizontally, and how they draw inspiration from natural processes through aleatoric methods. I also focused on the pioneering work of Iannis Xenakis, who spent a lifetime applying mathematical models to music, challenging traditional notions of composition and opening up new realms of possibility.
Today, an audio application extends far beyond the boundaries of a mere model; it encompasses a multidisciplinary fusion of mathematical theory, scientific understanding, sonic artistry, visual design, and product development. My journey, from my early academic studies on Xenakis’s work to the current iterations of my Cosmosf applications, reflects over 20 years of dedicated development and practical application, yet it remains a work in progress.
Generative audio is not only a tool for composition but also a reflection of the human desire to understand, explore, and recreate the dynamic, emergent properties of the universe itself. This approach invites us to consider music not just as a crafted object but as a living process, continuously shaped by both the algorithms that drive it and the creative minds that wield these tools. As we move forward, this dialogue between technology, art, and nature will continue to expand, offering new ways to engage with sound and redefine the boundaries of music itself.
The journey continues, guided by curiosity, innovation, and a relentless pursuit of new possibilities.
Sinan Bökesoy
Sinan Bökesoy is a composer, sound artist and principal developer of sonicLAB and sonicPlanet. Holding a Ph.D. in computer music from the University of Paris8, under the direction of Horacio Vaggione, Bökesoy has carved a niche for himself in the synthesis of self-evolving sonic structures. Inspired by composer greats such as Xenakis, his work leverages algorithmic approaches, mathematical models, and physical processes to generate innovative audio synthesis results. Bökesoy strives to establish a balanced workflow that bridges theory and practice, as well as artistic and scientific approaches. Bökesoy has presented his work at prestigious venues such as Ars Electronica / Starts Prize, IRCAM, Radio France Festival, and international biennials and art galleries. He has published and presented multiple times at conferences including ICMC, NIME, JIM, and SMC, as well as in the Computer Music Journal, MIT Press.
Article topics
Article translations are machine translated and proofread.
Artikel von Sinan Bökesoy
 Sinan Bökesoy
Sinan Bökesoy