36 Minuten
Der Begriff „Generative Audiosynthese“ bezieht sich auf einen Prozess, bei dem Computer bei der Klanggestaltung und der Berechnung von Klangstrukturen helfen. Diese Prozesse können vollständig automatisiert sein oder dem Komponisten eine erhebliche Kontrolle ermöglichen, wobei ein Gleichgewicht zwischen algorithmischer Autonomie und kreativer Leitung besteht.
Im 20. Jahrhundert begann die zeitgenössische Musiklandschaft, die Grenzen zwischen dem Komponieren des Klangs selbst und dem Komponieren mit Klang zu verwischen. Die Komposition von Klangfarben wurde zu einem strukturellen Element. Diese Entwicklung ergab sich aus dem Zugang zur Klanggestaltung durch den Umgang mit aufgezeichnetem Material –wie etwa die Organisation mehrerer Schichten von Klangelementen durch die Montage von Tonbandspulen. Angefangen mit manuellen Operationen in Studios wie dem WDR (Westdeutscher Rundfunk) und der GRM (Groupe de Recherches Musicales), erweiterte die Einführung von Computerhardware und Softwaretools die Möglichkeiten der Klangsynthese und der Verwendung von Klängen als Material für Kompositionen exponentiell. Es gab nicht nur einen Weg, ein Ziel. Das Studium der Komposition des Klangs und der Komposition mit dem Klang hat die Möglichkeiten verschiedener Schulen, Ästhetiken und Techniken vom Nachkriegsserialismus bis zum Ambient Sound Design ausgeweitet.
Ich bin Sinan Bokesoy. Ich begann mein Studium der elektronischen Musik am Centre de Création Musicale Iannis Xenakis in Paris und promovierte an der Universität Paris unter der Leitung von Horacio Vaggione mit dem Schwerpunkt auf sich selbst entwickelnden Klangstrukturen. In den letzten 25 Jahren habe ich mich der Erforschung algorithmischer Ansätze in der Komposition und im Sounddesign gewidmet und mit den von mir gegründeten Unternehmen sonicLAB/sonicPlanet professionelle Audioanwendungen entwickelt. Mein Ziel war es immer, einen ausgewogenen Arbeitsablauf zu schaffen, der Theorie und Praxis sowie künstlerische und wissenschaftliche Ansätze miteinander verbindet.
Generative Audiotechnik umfasst mehrere Disziplinen: die Wissenschaft des Klangs, Mathematik, Physik, Kompositionstheorien und das Wissen und die praktische Erfahrung, diese als Künstler anzuwenden. Selbst wenn man sich nur auf einen kleinen Teil dieses riesigen Bereichs konzentriert, kann es ein ganzes Leben an Forschung und Kreation erfordern, um rigorose Ergebnisse zu erzielen. Dies gilt insbesondere für die kontinuierliche Bewertung, Verfeinerung und Wiederholung von Ideen und Theorien, die eine der Hauptaktivitäten in meinem Entwicklungsprozess darstellen. Ich gehe in diesem Artikel weder von einem rein akademischen Niveau aus noch aus der Perspektive eines Anfängers, sondern eher aus einer Zwischenperspektive, die für diejenigen geeignet ist, die ein grundlegendes Verständnis haben und tiefere Einblicke suchen.
Das Konzept des Generativen
Wie verwandeln sich kalte Berechnungen in fesselnde Klanglandschaften oder organisierte musikalische Formen?
Generative Prozesse in der Musik, das Konzept der Nutzung von Verfahren zur Übersetzung von Informationen für kreative Zwecke, gibt es schon seit Jahrhunderten. Guido d'Arezzo (990–1033) beispielsweise entwickelte ein Modell, bei dem er Vokale aus einem Text bestimmten Tonhöhen zuordnete (Abbildung 1) und so melodische Phrasen schuf, die der Bedeutung der gesungenen Worte gerecht wurden. Die Übersetzung der phonemischen Struktur eines Textes in die Tonhöhen eines Plainsong mit der folgenden Zuordnung:
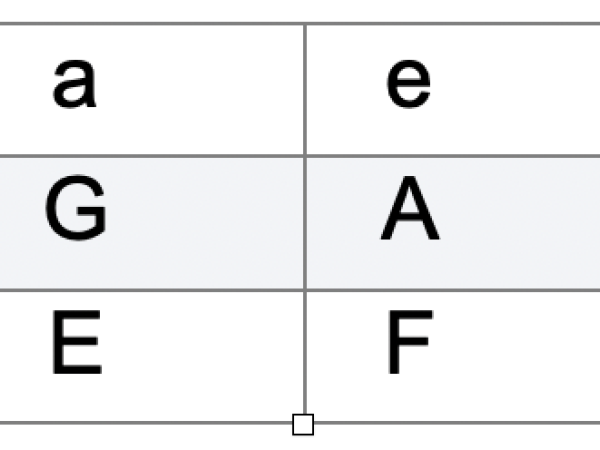
Abbildung 1. Zuordnung von Vokalen zu Tonhöhenwerten.
Dies ist ein frühes Beispiel dafür, wie strukturierte Regeln angewendet werden können, um eine musikalische Abbildung zu erzeugen. Wer kann leugnen, dass die Fugentechnik in den Händen von J.S. Bach (1685–1750) ein bemerkenswertes Beispiel für ein kompositorisches generatives Modell ist? Sie trug dazu bei, einige der schönsten Werke der Musik zu schaffen, indem sie einen strukturierten Rahmen für die vertikale und horizontale Organisation musikalischer Ideen bot, eine Art mehrdimensionales Mapping für Kreativität und Komplexität.
In unserem Jahrhundert beschreibt der Begriff „generativ“ im Bereich des computergestützten Sounddesigns und der Komposition einen kreativen Ansatz, bei dem Musik oder Klangelemente algorithmisch erzeugt werden, wobei der Mensch nur minimal eingreift und lediglich die anfänglichen Parameter oder Regeln festlegt. Diese Methode stützt sich auf Systeme, die durch Algorithmen autonom Inhalte generieren oder entwickeln können, wobei sie sich oft auf bestimmte Strukturen und Bedürfnisse konzentrieren, z. B. kontrollierte Zufälligkeit, prozedurale Regeln, Modelle physikalischer Prozesse, Variationen maschinell erlernter Modelle (generative KI), computergestützte Techniken, die die Stärke des Computers bei der Verarbeitung von Zahlen ausnutzen.
Durch den Einsatz dieser generativen Prozesse können Komponisten und Sounddesigner Klangtexturen, -muster und -strukturen erforschen, die mit manuellen Methoden unerreichbar wären.
Algorithmen dienen als zielgerichtete Rezepte, die Funktionsblöcke kombinieren, um bestimmte Aufgaben zu erfüllen. Das Flussdiagramm von Computersoftware ist natürlich genauso aufgebaut, es gibt einen Anfang und ein Ende, die Eingabe und die Ausgabe.
Obwohl die Algorithmen recht einfach strukturiert sein können, können sie auch komplexe Ergebnisse liefern, die viele prozedurale oder evolutionäre Prozesse aus der Natur widerspiegeln. Es ist jedoch wichtig, die generative KI von diesen Algorithmen zu unterscheiden, da sie sehr komplex und undurchsichtig ist. Die Erstellung eines Modells für maschinelles Lernen umfasst mehrere Schritte, von der Vorbereitung der Trainingsdaten über den Trainingsprozess bis hin zur Bewertung des Modells, die sich nicht in Form von Operationsblöcken wie oben beschrieben darstellen lassen.
Die schönste und komplizierteste Kunst entsteht oft aus einfachen Grundideen, ähnlich wie evolutionäre Prozesse in der Natur. Die Evolution zeigt, wie Komplexität aus einfachen Prinzipien – wie Variation, Selektion und Replikation – entstehen kann, die im Laufe der Zeit und auf verschiedenen Ebenen angewendet werden (fraktale Strukturen). Die Anwendung dieses Konzepts auf den Bereich der algorithmischen Komposition und der generativen Musik legt nahe, dass die zugrundeliegenden Algorithmen und mathematischen Prinzipien oft in eine Reihe von einfachen, aber effektiven Schritten destilliert werden können. Die Eleganz dieses Ansatzes liegt darin, dass unnötige Komplexität in der Struktur des Algorithmus selbst vermieden wird, sodass Reichtum und Tiefe aus der Interaktion dieser einfachen Regeln im Laufe der Zeit entstehen können. Zu viel Komplexität zerstört sich selbst, und es ist eine Tugend, dies beim algorithmischen Entwurf zu vermeiden.
Vor- Computer- Methoden
Von Edgar Varese über Luigi Russolo bis hin zu Pierre Schaeffer bestand die Motivation für die Verwendung neuer Klänge darin, eine Bresche in die Festung der musikalischen Tradition zu schlagen, wobei jede Kreation ein persönliches Manifest darstellt. Die Motivation: Werkzeuge zur Unterstützung der Klanggestaltung zu schaffen und nicht eine Maschine zu erfinden, die die kompositorische Aufgabe anstelle des Komponisten übernehmen kann.
Wie György Ligeti einmal bemerkte: „Ein Computer wird nicht von sich aus eine Komposition schaffen; es ist die Interaktion zwischen dem Komponisten und dem Computer, die die Komposition schafft." Im Kontext der heutigen Technologie können wir in der Tat komplexe und autonome Systeme bauen, aber der generative Prozess sollte idealerweise immer noch als ein Instrument funktionieren, mit dem der Komponist interagiert, und nicht als ein monolithisches, in sich geschlossenes System.
Wenn wir über unsere jüngste Vergangenheit nachdenken, gibt es eine Zeit, in der es praktisch keine digitalen Mittel für die Aufzeichnung von Audio gibt. Komponisten experimentierten mit elektronischem Klang durch manuelle Operationen, wie das Zerschneiden von Tonbandaufnahmen (konkretes Material) in analogen Umgebungen, um mehrere Schichten mit polyrhythmischen Strukturen, vertikalen und horizontalen Komplexitäten und sich entwickelnden Klangtexturen zu konstruieren. Tongeneratoren wurden eingesetzt, um postserielle Cluster zu erzeugen und den Klang von seiner Quelle zu abstrahieren, indem verschiedene Kontexte zusammengeführt wurden.

Figure 3. Pre-DSP age electronic music labs.
Bis dahin hatte der Prozess der Musikschöpfung keine plastischen Qualitäten – Komponisten konzipierten Musik und schrieben dann Zeichen auf Papier, die den stabilen Frequenzen der für die Aufführung bestimmten Musiknoten entsprachen. Die mit Tonbandgeräten vorbereitete und komponierte Musik hingegen konnte nicht vorher existieren, sondern war ein Produkt der aufgezeichneten Elemente, aus denen sie bestand. Ähnlich wie die Werkzeuge eines Tischlers/Bildhauers, der sein Werk durch Manipulation des Materials mittels physikalischer Prozesse formt, boten diese elektronischen Musiklabors (Abbildung 3) die ersten Umgebungen, in denen Komponisten das Klangmaterial umgestalten und ihre kompositorische Form schaffen konnten.
Diese Überlagerung und Verarbeitung von Klangmaterial ermöglichte die Erforschung der Klangentstehung und bot unschätzbare Erfahrungen bei der Schaffung von Klangkompositionen, die über die traditionellen Orchesterklänge hinausgehen. Ligeti selbst räumte ein, dass seine Arbeit in den elektronischen Musikstudios des WDR für die Entwicklung der in seinem Stück Atmosphères (1961) verwendeten Techniken, insbesondere für die Erzeugung dichter Toncluster, von wesentlicher Bedeutung war. Der statische Charakter der elektronischen Musik spiegelt sich in der Klangtextur von Atmosphères wider, wo die vertikale Schichtung von Klangmaterialien auf Mikroebene eine kontinuierliche Kontrolle über die Spektralmorphologie des Klangs ermöglicht. Zahlreiche unabhängige musikalische Linien (Mikropolyphonie) verschmolzen und verwischten ihre Grenzen, und dieser Stil wurde zu einem Markenzeichen Ligetis. Der Grund, warum ich sein Werk Atmosphères erwähne, ist die allmähliche Umwandlung von Klangmassen, die sich organisch wie in Gasen bewegen und subtile Verschiebungen in Textur und Farbe ermöglichen. Abbildung 4 veranschaulicht die Massenbewegung und dynamische Struktur der Klangtextur von Atmosphères und zeigt deutlich, wie sie sich innerhalb der Tonhöhengrenzen entwickelt.
Wie lassen sich algorithmische Modelle erstellen, die die musikalische Struktur in mehreren Dimensionen formen?
Die Klangfarbe als Struktur hat mehrere Dimensionen, wobei Tonhöhe und Intensität nur die sich daraus ergebenden Ergebnisse sind. Die Herausforderung besteht darin, mehrere Schichten von Klangmaterial zu schaffen und sowohl die horizontale als auch die vertikale Struktur der Klangkomposition so zu gestalten, als wäre sie ein Instrument – eine intelligente Komposition von Zeit – und Wahrnehmungsinformationen, die unser auditorisches System anspricht.
Auch bei dem algorithmischen Ansatz zur Klangerzeugung im 20. Jahrhundert ging es nicht darum, Computer so zu programmieren, dass sie Variationen von Bach oder Debussy erzeugen. Vielmehr ging es darum, die Klangkomposition voranzutreiben, indem riesige Informationsmengen auf mikroskopischer Ebene verarbeitet, die Spektralstruktur des Klangs untersucht und diese Erkenntnisse in Kompositionen integriert wurden, die sowohl elektronische als auch akustische Elemente enthalten. Es geht um den Umgang mit Klang jenseits der traditionellen Notation, um die Verwendung abstrakter Werte und multimodaler Darstellungen.
Meine Auseinandersetzung mit diesen Themen ist in dem von mir gewählten akademischen Weg verwurzelt. Meine Auseinandersetzung mit elektronischer Musik begann durch die Werke von Iannis Xenakis am Centre de Création Musicale Iannis Xenakis während meines Kompositionsstudiums in Paris.
Inspiriert von den wissenschaftlichen Fortschritten in der Physik und Astronomie, betrachten Komponisten natürliche Prozesse als Inspirationsquellen. Der Zufall ist die Grundlage des Universums, von Quantenereignissen bis zur Organisation großer Teilchenstrukturen. Die Wissenschaft der Statistik wurde entwickelt, um diese Strukturen zu verstehen, zu kontrollieren, zu simulieren und vorherzusagen. Der ständige Fluss natürlicher Prozesse ist ein fruchtbarer Boden für die Entwicklung klanglicher Morphologie und klanglicher Bewegung als Elemente einer kontinuierlichen Komposition. Aleatorische oder zufällige Prozesse in der Musik sind seit langem ein Schwerpunkt der Avantgarde – Komponisten, die die Grenzen der Unvorhersehbarkeit ausloten.
John Cages Einsatz des Zufalls, inspiriert durch das I-Ching (ein alter chinesischer Wahrsagetext), spiegelt beispielsweise seine Philosophie wider, persönliche Befangenheit aus dem Kompositionsprozess zu entfernen. Indem er Zufallsoperationen wie das Werfen einer Münze oder Würfeln einsetzte, um Elemente wie Tonhöhen, Rhythmen oder Dynamik zu bestimmen, versuchte Cage, den Kompositionsprozess zu demokratisieren und allen Möglichkeiten die gleiche Chance zu geben, sich zu manifestieren. Dieser Ansatz deckt sich mit seinem Interesse am Zen- Buddhismus, der Akzeptanz, Offenheit und die Abwesenheit von Vorurteilen betont.
Cages Werke wie Music of Changes und 4'33 verdeutlichen sein Engagement für Unvorhersehbarkeit und die Einbeziehung aller Klänge – ob traditionell musikalisch oder aus der Umwelt – als Teil einer Komposition. Wie Heraklit schon sagte: „Man kann nicht zweimal in denselben Fluss steigen.“
Iannis Xenakis’ bahnbrechende algorithmische und mathematische Ansätze
Iannis Xenakis verfolgte einen einzigartigen und radikalen Kompositionsansatz, indem er sein Fachwissen in Musik, Architektur und Mathematik zusammenführte und so den Weg für generative und algorithmische Prozesse bereitete. Auch ohne die anfängliche Hilfe von digitalen Computern setzte Xenakis mathematische Methoden wie stochastische Prozesse, Mengenlehre und Spieltheorie ein, um seine Musik zu formalisieren. Seine Algorithmen, die durch analoge Berechnungen entstanden, zielten darauf ab, sich von traditionellen Formen und Konventionen zu lösen. In seinem Manifest stellte Xenakis sich vor, jede Komponente des Klangs und der musikalischen Komposition von vergangenen Paradigmen zu befreien. Für ihn bedeutete dies, vordefinierte Strukturen und Regeln abzuschütteln, um zu einer reinen Form der Kreativität zu gelangen, die auf mathematischer Logik, wissenschaftlichen Prinzipien und einer tiefgreifenden Auseinandersetzung mit den grundlegenden Elementen von Klang und Form beruht. Durch die Minimierung von Zwängen glaubte er, dass Künstler ein ursprünglicheres Verständnis von Musik und Kunst entwickeln könnten, das die natürlichen Prozesse und Kräfte widerspiegelt.
Xenakis setzte sich für die Verwendung mathematischer Modelle und probabilistischer Techniken ein, um musikalische Formen zu erzeugen, die unvorhersehbar sind, aber dennoch den zugrunde liegenden wissenschaftlichen Gesetzen unterliegen. Bei diesem Ansatz geht es nicht um die völlige Abschaffung von Regeln, sondern um die Auswahl der einfachsten, grundlegendsten Beschränkungen, die die Komplexität der natürlichen Welt widerspiegeln. Xenakis glaubte, dass Künstler auf diese Weise Werke schaffen können, die dynamischer und organischer sind und mit den Kräften und Mustern der Natur in Einklang stehen.
Xenakis übersetzte mathematische Daten in Tonbandmanipulationen und Orchestrierung für akustische Instrumente. Seine Kompositionen sind bekannt für ihre komplexen Schichten und die Verwendung mathematischer Modelle zur Gestaltung der Dichte, Dynamik und Entwicklung von Klangmassen im Laufe der Zeit. Darüber hinaus sind diese Techniken in seinen Kreationen sehr transparent, sei es um komplexe Texturen oder Formen in Stücken wie Metastasis oder Achorripsis zu schaffen. Ich möchte nun eine Aufschlüsselung der mathematischen Konzepte vorstellen, die seinen Kompositionen Metastasis, Achorripsis und Concrete PH zu Grunde liegen.
“Metastasis (1953-54)”
"Metastasis" kann als "jenseits der Unbeweglichkeit" oder "Veränderung nach dem Stillstand" verstanden werden. Im Kontext der Komposition bezieht sich "Metastasis" auf die allmähliche Umwandlung von Klangmassen im Laufe der Zeit. In Metastasis setzte Xenakis stochastische Prozesse ein, um die Glissandi (kontinuierliche Tonhöhenverschiebungen) der Streichinstrumente zu strukturieren. Er wandte statistische Methoden an, um die Dichte und Dynamik der Massen zu kontrollieren, was ein Gefühl der Zufälligkeit und Unvorhersehbarkeit erzeugte, während er sich an ein zugrundeliegendes probabilistisches Modell hielt. Dieser Ansatz spiegelt die natürlichen Phänomene komplexer Systeme wider, z. B. die Muster von Vogelschwärmen oder die Bewegungen von Menschenmengen, bei denen einzelne Elemente scheinbar zufällig agieren (Mikroebene), aber gemeinsam kohärente Strukturen bilden. (Makro-Skala)
Zur Steuerung der Bewegung von Klangmassen verwendete Xenakis Gaußsche (oder normale) Verteilungen (Abbildung 5). Damit konnte Xenakis die Ausbreitung und Konvergenz von Klangereignissen modellieren, was zu sich entwickelnden Klanglandschaften führte, die natürlichen Prozessen wie der Flüssigkeitsdynamik oder der thermischen Diffusion ähneln.
Die Gauß-Verteilung, auch als Normalverteilung bekannt, ist eine statistische Funktion, die am besten durch ihre glockenförmige Kurve charakterisiert ist, die beschreibt, wie eine Reihe von Werten symmetrisch um einen zentralen Punkt, den sogenannten Mittelwert (μ), verteilt ist. Die meisten Werte sind um den Mittelwert gruppiert, und die Wahrscheinlichkeit von Werten, die weiter vom Mittelwert entfernt sind, nimmt exponentiell ab. Sie ist eine der wichtigsten Wahrscheinlichkeitsverteilungen in der Statistik, da sie in vielen realen Phänomenen vorkommt. Die Formel lautet wie folgt:
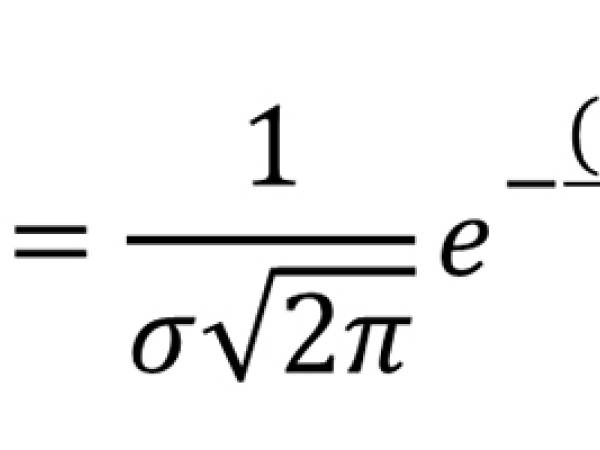
Bei der Verwendung in Metastasis steht x für einen bestimmten musikalischen Parameter (z. B. Tonhöhe oder Dauer), μ ist der Mittelwert (Durchschnittswert, um den sich die Ereignisse gruppieren), und σ ist die Standardabweichung (die die Streuung oder Konzentration um den Mittelwert herum bestimmt) und wurde verwendet, um die Wahrscheinlichkeit zu berechnen, dass bestimmte musikalische Ereignisse zu bestimmten Zeiten oder Tonhöhen eintreten. Xenakis passte diese Parameter (μ und σ) an, um die musikalische Textur dynamisch zu gestalten, indem er entschied, wo die Klangereignisse stärker gebündelt oder gestreut auftreten sollten.
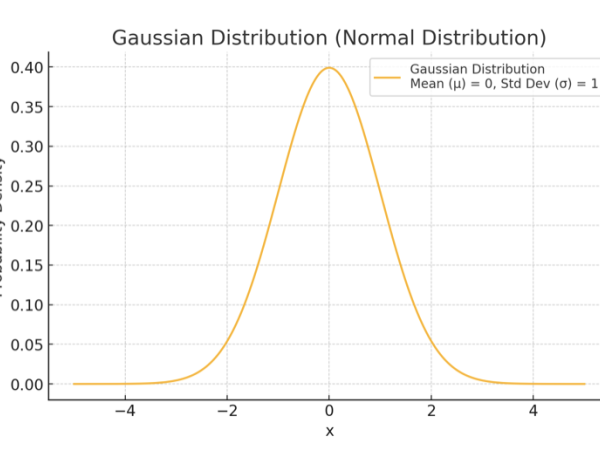
Figure 5. The bell-shaped distribution curve of events in Gaussian distribution.
Tonhöhen und Glissandi: Xenakis ist dafür bekannt, dass er kontinuierliche Tonhöhenverläufe auf Streichinstrumenten erzeugt. (Abbildung 6) Die Partitur von Metastasis zeigt diese Bewegungen, wie Sie in der Abbildung oben sehen können. Durch die Verwendung von Gaußschen Verteilungen zur Kontrolle der Tonhöhe und der Dichte der Glissandi (kontinuierliche Übergänge zwischen den Tonhöhen) wurden die Anfangs- und Endpunkte dieser Glissandi, die Geschwindigkeit ihrer Bewegung und ihre Konzentration innerhalb bestimmter Zeitrahmen bestimmt. Zum Beispiel wurden die itches entsprechend der Glockenkurve der Gaußschen Verteilung verteilt, bei der sich die meisten Ereignisse um eine zentrale Tonhöhe gruppieren und weniger Ereignisse bei extrem hohen oder tiefen Tonhöhen auftreten. So entstand eine Textur, bei der die Klangereignisse in der Mitte konzentriert sind und sich allmählich zu den höheren und tieferen Lagen hin ausbreiten, was die Ausbreitung von Partikeln in einer Flüssigkeit imitiert.
Dauer und Dynamik: Die Gauß-Verteilung beeinflusst auch die Dauer und Dynamik von Schallereignissen, sodass Muster entstehen, bei denen die Dauer von Tönen oder Klangmassen häufiger um einen zentralen Wert herum liegt, während kürzere oder längere Dauern immer seltener werden. Auch die Dynamik (Lautstärke) dieser Ereignisse konnte so gestaltet werden, dass sich die meisten Klänge um eine mittlere Intensität gruppieren und weniger Klänge bei sehr leisen oder sehr lauten Pegeln auftreten. Diese probabilistische Gestaltung gab dem Stück ein Gefühl von organischem Fluss, bei dem sich Dichte und Intensität im Laufe der Zeit natürlich entwickelten.
Dichte der Klangereignisse: In Xenakis’ Kontext bezieht sich Dichte" auf die Anzahl der Klangereignisse, die innerhalb einer bestimmten Zeitspanne auftreten, und auf die räumliche Verteilung dieser Ereignisse über das Tonhöhenspektrum. Mit Hilfe der Gauß'schen Verteilung konnte bestimmt werden, wie dicht oder locker diese Ereignisse zu einem bestimmten Zeitpunkt gepackt waren.

Figure 6. “Metastasis” score bars 317-333. Source: Iannis Xenakis, Musique, Architecture, Tournai, Castermann. 1976 p.8
In klimatischen Abschnitten würde die Verteilung zum Beispiel eine hohe Dichte an Klangereignissen ergeben, die sich zusammenballen und eine dichte, strukturierte Klangmasse erzeugen. Im Gegensatz dazu würde die Verteilung in ruhigeren oder weniger dichten Abschnitten die Ereignisse spärlicher verteilen, wodurch ein Gefühl von Raum und Offenheit entsteht. Mit dieser Methode konnte Xenakis Klangmassen so modellieren, dass sie dem Verhalten von Teilchen unter verschiedenen Kräften ähneln, was zu sich entwickelnden Klanglandschaften mit flüssigkeitsähnlicher Dynamik führt.
Xenakis’ Hintergrund in der Architektur, insbesondere seine Zusammenarbeit mit Le Corbusier beim Philips-Pavillon, beeinflusste die strukturelle Gestaltung von Metastasis. Die Partitur des Werks (siehe Beispielbild oben) enthält eine grafische Notation, die architektonischen Entwürfen ähnelt und hyperbolische Paraboloide verwendet – eine Form, die im Design des Pavillons verwendet wurde. Xenakis wandte diese geometrischen Konzepte an, um die Tonhöhe und den dynamischen Verlauf der musikalischen Ereignisse zu steuern, und behandelte sie als architektonische Strukturen, die sich im Laufe der Zeit entwickeln.

Figure 7. Comparing the architecture of Phillips Pavilion and the score of Metastasis.
Concrete PH (1958)
Concrete PH (1958) ist eines der bahnbrechenden Werke von Iannis Xenakis in der elektronischen Musik. Es ist ein Beispiel für musique concrète, bei dem das Klangmaterial vollständig aus manipulierten Aufnahmen besteht, die mit innovativen Techniken der Klangmanipulation bearbeitet wurden.
Vorläufer der Granularsynthese: Concrete PH gilt als eines der ersten Stücke, das eine der Granularsynthese ähnliche Klangtextur aufweist und damit sowohl der Terminologie als auch der damit typischerweise verbundenen digitalen Technologie vorausging. Xenakis erreichte dies, indem er winzige Segmente von Tonaufnahmen aus brennender Holzkohle auf Magnetband akribisch bearbeitete und neu anordnete (Abbildung 8). Die brennende Holzkohle wurde mit Bedacht gewählt; sie bot eine natürliche Klangquelle, die sich durch ein chaotisches Muster von Knistern und Knacken auszeichnet, das einer zufälligen Verteilung von Ereignissen ähnelt. Dieses Rohmaterial war ein idealer Kandidat für Xenakis’ Erforschung stochastischer Prozesse.
Er zerlegte diese Aufnahmen in kleine, halbsekündige Fragmente und manipulierte deren Tonhöhen und Dynamik, so dass eine dichte, strukturierte Klangmasse entstand, die organische Prozesse nachahmte. Dieser innovative Ansatz nutzte statistische Methoden und manuelle Bandmanipulation, um aus einfachen Elementen komplexe Klangstrukturen zu schaffen.

Figure 8. Xenakis working in studio on Bohor, 1962.
Statistische Verteilungen und manuelle Berechnungen: Xenakis verwendete Poisson-Verteilungen, um das Auftreten dieser Klangkörner im Laufe der Zeit zu modellieren. Die Poisson-Verteilung ist eine Wahrscheinlichkeitsverteilung, die die Anzahl der Ereignisse beschreibt, die innerhalb eines festen Zeit- oder Raumintervalls auftreten, wenn diese Ereignisse unabhängig voneinander und mit einer konstanten Durchschnittsrate auftreten. Im Gegensatz zur Gauß-Verteilung, die kontinuierlich ist, ist die Poisson-Verteilung diskret, d. h. sie befasst sich mit ganzen Zahlen (z. B. mit der Anzahl der Ereignisse):
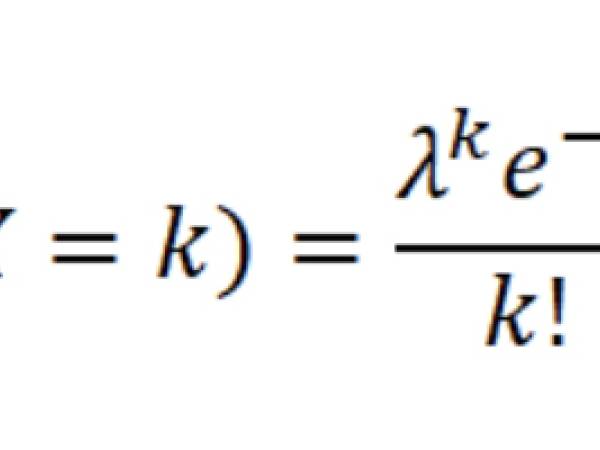
In einer Poisson-Verteilung (Abbildung 9) stellt der Mittelwert (λ, lambda) sowohl die erwartete Anzahl der Ereignisse (die durchschnittliche Rate) als auch die Varianz (die Streuung der Ereignisse um den Mittelwert) dar. Das bedeutet, dass, wenn die durchschnittliche Häufigkeit der Ereignisse λ ist, die Varianz der Verteilung ebenfalls λ ist.
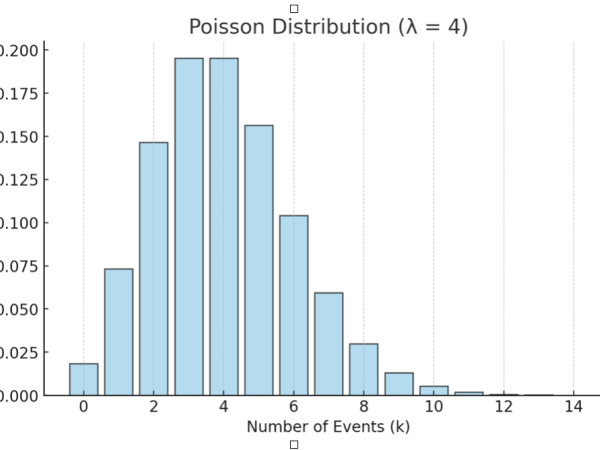
Figure 9. The Poisson distribution for discrete events.
Die Poisson-Verteilung wird häufig verwendet, um die Anzahl von Ereignissen zu modellieren, die innerhalb eines bestimmten Zeitraums oder einer bestimmten Region auftreten, z. B. die Anzahl der Anrufe, die in einer Stunde bei einem Callcenter eingehen, die Anzahl der Autos, die an einem Tag eine Mautstelle passieren, oder sogar die Anzahl der Klangereignisse in einem Abschnitt einer Komposition, wie es Xenakis tat. Diese Verteilung war geeignet, die zufällige und sporadische Natur des Knisterns von Holzkohle zu modellieren, bei dem einzelne Schallereignisse im Laufe der Zeit unvorhersehbar auftreten. Durch die Anwendung der Poisson-Verteilung konnte er die Dichte der Klangereignisse – die Anzahl der pro Zeiteinheit auftretenden Klangkörner – kontrollieren, ohne eine feste rhythmische Struktur vorzuschreiben. Auf diese Weise erschienen die Klänge zufällig verteilt, ähnlich wie das Muster von Regentropfen, die auf eine Oberfläche treffen, oder von Teilchen, die sich in einem Gas bewegen. (Abbildung 10)
Mikroklang und Klangpartikel: In Concrete PH konzipierte Xenakis den Klang als "Mikroklang" oder winzige Klangpartikel. Jedes Teilchen oder Klangkorn wurde wie ein Molekül in einem Gas behandelt, das mit anderen nach stochastischen Regeln interagiert. Indem er stochastische Verteilungen sowohl auf die Zeitintervalle als auch auf die Parameter der Klangkörner anwandte, schuf Xenakis eine Komposition mit mehreren Ebenen der Komplexität. Der probabilistische Ansatz ermöglichte es ihm, die Dichte, Dauer, Tonhöhe und Dynamik von Klangereignissen so zu gestalten, dass sie natürlichen chaotischen Prozessen wie dem Knistern von Feuer oder Wassertropfen sehr nahekommen. Das Ergebnis ist eine Klangtextur, die sowohl zufällig als auch kohärent erscheint, da sie den in der Natur beobachteten statistischen Mustern folgt.
Integration von mathematischen und räumlichen Konzepten: Der Titel "PH" bezieht sich auf den Philips-Pavillon, der von Xenakis und Le Corbusier für die Weltausstellung 1958 in Brüssel entworfen wurde und in dem das Stück uraufgeführt wurde. Die Komposition wurde so konzipiert, dass sie mit der charakteristischen Akustik und der geometrischen Struktur des Pavillons interagiert und Xenakis’ Interesse an der Verschmelzung mathematischer und physikalischer Modelle in verschiedenen Bereichen widerspiegelt. Die einzigartigen Formen und Oberflächen der Architektur beeinflussten die Ausbreitung des Klangs im Raum und machten Concrete PH zu einem frühen Beispiel für raumbezogenes Sounddesign, das die Musik mit ihrer physischen Umgebung verbindet.
Innovativer Einsatz von Tonbandmanipulation: In Concrete PH erforschte Xenakis die Möglichkeiten des Magnetbands, der fortschrittlichsten Audiotechnologie seiner Zeit. Xenakis berechnete akribisch die Wahrscheinlichkeiten und Verteilungen, um seine Manipulation des Magnetbandes zu steuern. Er schnitt, spleißte und variierte die Abspielgeschwindigkeiten der Bandfragmente manuell nach diesen Berechnungen und setzte so seine stochastischen Methoden mit der damals verfügbaren Technologie um. Diese analogen Techniken legten den Grundstein für künftige Entwicklungen in der elektronischen Musik und zeigten, wie mathematische und statistische Ansätze auf die Klangmanipulation angewendet werden konnten, um innovative Texturen und Klangformen zu schaffen.
Xenakis komponierte mehr Orchesterwerke als elektronische Musikstücke, was in erster Linie auf die damaligen technischen Beschränkungen zurückzuführen war. Das Fehlen von Personalcomputern und fortschrittlichen Programmierumgebungen machte es schwierig und arbeitsintensiv, die riesigen Datenmengen zu verarbeiten, die für die Bandmanipulation und die Klangsynthese erforderlich waren. Außerdem wurden die abstrakten numerischen Daten, die er durch seine Berechnungen erzeugte, einem strengen Kompositionsprozess unterzogen. Xenakis ordnete diese mathematischen Ergebnisse akustischen Instrumenten zu, legte die Orchestrierung fest und definierte die Elemente der Klangtextur, was zu einer progressiven Entwicklung seiner Kompositionen führte. Das endgültige Werk ist also nicht einfach das Ergebnis eines Algorithmus, sondern das Produkt von Xenakis’ kreativem Prozess, bei dem er den algorithmischen Rahmen entwarf und die Ergebnisse dann durch eine bewusste kompositorische Strategie integrierte.
Xenakis hat seine mathematischen Modelle ständig erweitert und sie in seiner Tonbandmusik, Orchestermusik und später in seinen Computersoftwareentwicklungen zur Klangsynthese auf Wellenformebene angewendet.
Achorripsis ( 1956 - 57 )
In Achorripsis, einer Kreation für Orchesterinstrumente, hat er Markov-Ketten zur Steuerung von Übergängen zwischen aufeinanderfolgenden Zeitabschnitten eingeführt und damit eine Form der Erzählung oder Evolution geschaffen, die für die Erzeugung komplexer Texturen und Strukturen berechnet ist, welche die Kohärenz aufrechterhalten und gleichzeitig ein hohes Maß an Variabilität zulassen.
Seine Kompositionen Achorripsis, Analogique A und B sind lediglich Beispiele für die Verwendung all dieser Modelle und werden in seinem Buch Formalized Music ausführlich beschrieben.
Nehmen Sie einen Zeitrahmen von bestimmter Länge, etwa einen Takt. Wir möchten einige Schallereignisse innerhalb dieses Zeitrahmens verteilen. Wie viele Ereignisse? Und wann beginnen und enden sie?
Wir können uns dies als eine Top-down-Organisation der Ereignisse vorstellen, die mit einem Zeitrahmen auf Makroebene beginnt und die Ereignisse in diesem Raum verteilt. Xenakis hat die Poisson-Wahrscheinlichkeitsverteilung gewählt, um zu entscheiden, wie viele Ereignisse sich in diesem Raum befinden sollen, und zwar aus den oben erläuterten Gründen. Ausgehend von einem Mittelwert verteilt die Poisson-Formel die Dichtewerte um diesen Wert herum.
Für den Beginn und die Dauer von Ereignissen hat Xenakis die Exponentialverteilung verwendet, im Gegensatz zur Poisson-Verteilung, die eine kontinuierliche Verteilung ist. Die Exponentialverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die häufig verwendet wird, um die Zeit zwischen unabhängigen Ereignissen zu modellieren, die mit einer konstanten durchschnittlichen Rate auftreten.
Eine der Schlüsseleigenschaften der Exponentialverteilung ist ihr "gedächtnisloser" Charakter, d. h. die Wahrscheinlichkeit, dass ein Ereignis in der Zukunft eintritt, ist unabhängig von allen vergangenen Ereignissen. Die Formel lautet wie folgt und die Verteilung ist in Abbildung 11 dargestellt.

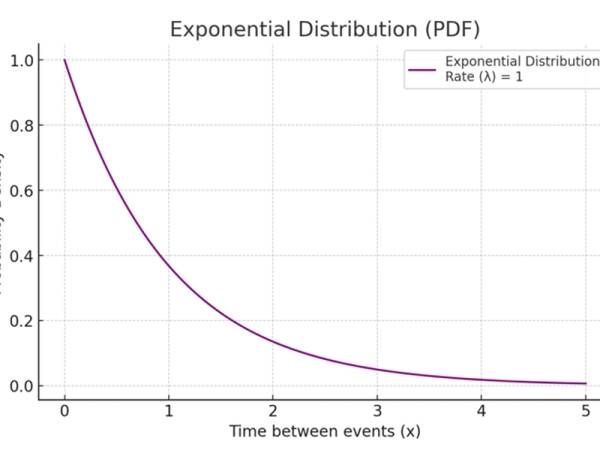
Figure 11. An example uses case of Exponential distribution modeling the probability versus the time between events.
In Abbildung 12 sehen Sie eine Beispielverteilung von Ereignissen, bei der die Dichte mit der Poisson-Verteilung, die Anfangs-/Dauerwerte mit der Exponentialverteilung und die Glissandi-Rampen mit der Gauß-Verteilung berechnet wurden.
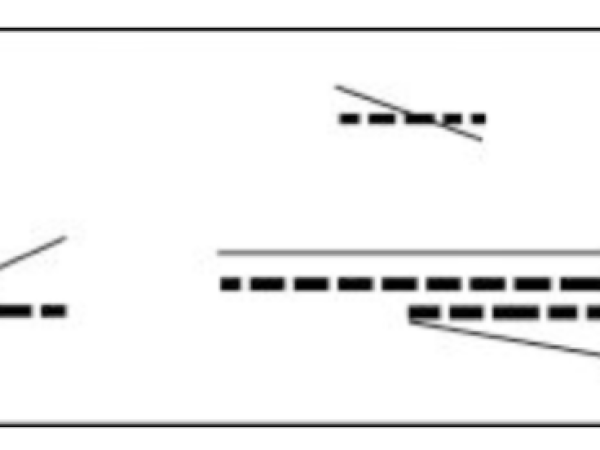
Figure 12. A time frame / cell with distributed events.
Nach diesem Schritt erhält jede verteilte Einheit eine Identität mit Parametern wie Tonhöhe und Intensität. Nach Xenakis hat eine klangliche Einheit einen mehrdimensionalen Vektorzustand im klanglichen Raum. Die Bewegung von einem Punkt zum anderen ist eine kontinuierliche Operation auf der Mikroebene. (Abbildung 13) Während einzelne Ereignisse auf der Mikroebene unvorhersehbar sein können (wie der Wurf eines einzelnen Würfels), kann das Gesamtverhalten einer Masse von Ereignissen kontrolliert und manipuliert werden, um auf der Makroebene einen gewünschten musikalischen Effekt zu erzielen. Dies sind Übergangsgesten zwischen Ordnung und völliger Zufälligkeit/Chaos.
Xenakis verwendet den Markov-Prozess, um eine Änderung ausgewählter Parameter in der Abfolge der Bilder zu berechnen. Der Markov-Prozess ist eine stochastische Methode, bei der die Wahrscheinlichkeit eines zukünftigen Zustands nur vom aktuellen Zustand abhängt, nicht aber von der Abfolge der Ereignisse, die i t vorausgegangen sind. Dieser Ansatz eignet sich besonders für die Modellierung dynamischer Systeme, die sich im Laufe der Zeit auf der Grundlage bestimmter Wahrscheinlichkeiten entwickeln, wodurch auch eine gewisse Abhängigkeit zwischen den Ereignisrahmen hergestellt wird.
Xenakis unterteilt Achorripsis in 28 verschiedene Zeit-/Ereignisrahmen oder "Abschnitte". Jeder Abschnitt ist durch verschiedene musikalische Parameter wie Tonhöhe, Dynamik, Klangfarbe und Dichte (die Anzahl der Klangereignisse) gekennzeichnet. Die Übergänge zwischen diesen Abschnitten werden durch eine Markov-Kette gesteuert, die die Wahrscheinlichkeit des Wechsels von einem Parametersatz zu einem anderen bestimmt. Hier verwenden wir eine Matrix von Wahrscheinlichkeiten, die gibt vor, welcher Zustand (Kombination von musikalischen Parametern) auf den aktuellen Zustand folgen wird, wodurch ein gewisses Maß an Unvorhersehbarkeit gewährleistet wird, während gleichzeitig ein strukturierter Rahmen eingehalten wird.
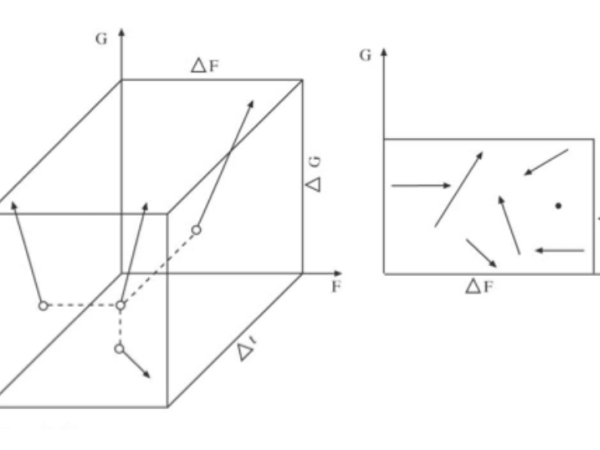
Figure 13. A sonic entity is defined as a vector with 3 dimensions.
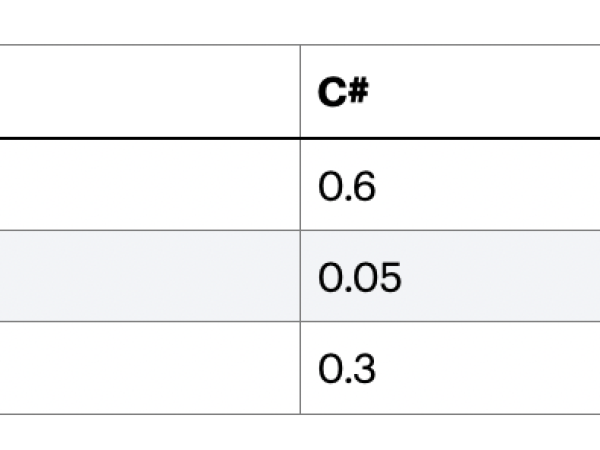
Figure 14. An example Markovian matrix defining transitions between pitch values.
Bitte beachten Sie, dass die Summe jeder Zeile 1 sein muss, was bedeutet, dass eine dieser 3 Möglichkeiten mit Sicherheit gewählt wird. Wir können ablesen, dass ein Übergang von der Note A zu A eine Wahrscheinlichkeit von 10% hat, und von der Note A zu C# eine Wahrscheinlichkeit von 60%. Und wenn wir die Übergänge C# zu C# und Eb zu Eb betrachten, können wir sagen, dass diese Matrix keine große Chance bietet, dass sich eine Note wiederholt. Genau wie bei der teilweisen Modellierung serieller Musik!
In Abbildung 15 sehen Sie die Achorripsis-Matrix für die Verteilung der Ereignisdichte auf die Instrumentenabschnitte.
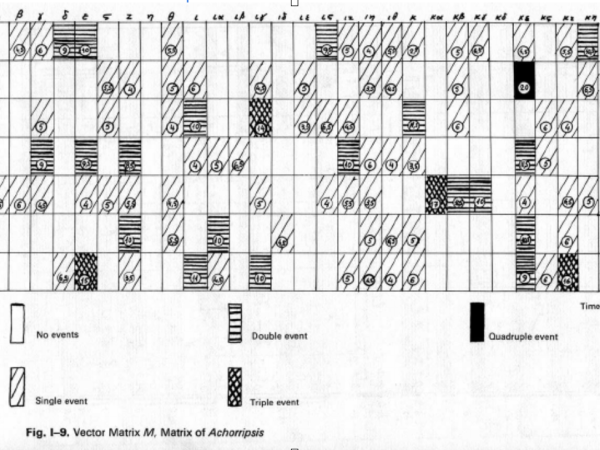
Figure 15. Xenakis description of Achorripsis density transitions over instrumental groups.
In Abbildung 16 hat Xenakis die Übergangswahrscheinlichkeiten von Häufigkeit, Intensität und Ereignisdichten für jeden Zeitrahmen klar notiert.

Figure 16. Xenakis's description of frequency, intensity, and density transition matrices.
Der Markov-Prozess enthält einen speziellen Zustand, der als Ziel- oder Absorptionszustand bezeichnet wird. Sobald der Prozess diesen Zustand erreicht, geht er nicht nach den normalen Regeln in einen anderen Zustand über, sondern löst einen Neustart aus. Wenn die Markov-Kette den Zielzustand erreicht, wird sie auf einen Ausgangszustand oder einen vordefinierten Satz von Anfangsbedingungen "zurückgesetzt".
Dieser Neustart kann deterministisch sein (immer zum gleichen Zustand zurückkehren) oder probabilistisch (aus einer Reihe von Zuständen auf der Grundlage einer anfänglichen Wahrscheinlichkeitsverteilung wählen). Es ist ein Punkt, an dem der Komponist, z. B. Xenakis, in den generativen Prozess eingreifen kann. Nach dem Neustart beginnt der Markov-Prozess erneut und folgt demselben Satz von Übergangswahrscheinlichkeiten, bis er erneut den Zielzustand erreicht.
Dieser Zyklus wiederholt sich auf unbestimmte Zeit oder bis eine bestimmte Bedingung erfüllt ist, was verschiedene Variationen wiederkehrender Ereignisse ermöglicht. Er bietet dem Komponisten auch die Flexibilität, einen bevorzugten Übergangsprozess aus mehreren Alternativen auszuwählen.
Xenakis beschrieb seine Kompositionstechniken ausführlich in seinem Buch Formalized Music: Thought and Mathematics in Composition, erstmals 1971 bei Indiana University Press veröffentlicht und 1992 bei Pendragon Press neu aufgelegt. Meiner Ansicht nach ist dieses Buch ein grundlegender Text für die computergestützte Komposition. Das Studium dieses umfassenden Werks während meiner Studienzeit ermöglichte es mir, diese Modelle nachzubilden und ein tieferes Verständnis für sie zu gewinnen.
Meine Beiträge
Im Vergleich zu den technischen Mitteln, die Xenakis zur Verfügung standen, hatte ich 2001 Zugang zu einer Version von Max/MSP und einem Apple PowerBook G4. Beim Studium seiner Werke ging es mir nicht darum, seine Musik nachzubilden, sondern seine Modelle als Grundlage für die Entwicklung von Strukturen zu nutzen, die sich auf Klangsynthesetechniken mit zeitgenössischen digitalen Audiowerkzeugen anwenden lassen. Ich erinnere mich, dass ich eine Grundversion seines GenDyn-Oszillators (stochastische Wellenformsynthese) in Csound erstellte, aber bald darauf konzentrierte ich mich auf sein Achorripsis-Modell. Ein so komplexes System zur Erzeugung und Modulation von Ereignissen in Max/MSP zu entwickeln, war damals eine programmiertechnische Herausforderung, zumal ich eine interaktive und Echtzeit-Umgebung beibehalten wollte. Außerdem fehlten mir zu diesem Zeitpunkt die Fähigkeiten, eine C++-Anwendung zu programmieren.
Das Ergebnis war die Entwicklung der Anwendung "Stochos" (Abbildung 17), die auf großes Interesse stieß, wissenschaftlich veröffentlicht wurde und zur Komposition und Aufführung von Stücken auf wissenschaftlichen Konferenzen führte. Durch die Anwendung dieser Kompositionsmodelle in der Echtzeit-Audiosynthese wurden Texturen erzeugt, die mit manuellen Methoden unmöglich zu erreichen gewesen wären.
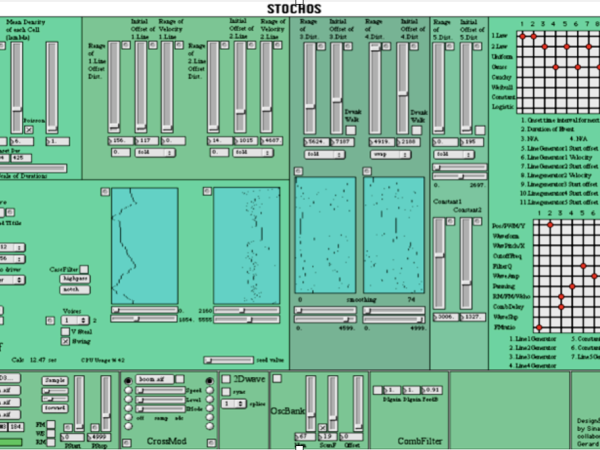
Figure 17. Stochos application developed on MaxMSP in 2001-2002.
Stochos enthielt keinen stochastischen Markov-Prozess, um die Übergänge zwischen aufeinanderfolgenden Zeitfenstern zu verwalten, sodass es keine Parameterabhängigkeit zwischen den Fenstern gab. (Abbildung 18) Es verfügte jedoch über ein Modell zur Erzeugung von Ereignissen, das die Dichte der Ereignisse, ihre Anfangszeiten, die Dauer und die Länge jedes Zeitrahmens mit Hilfe probabilistischer Verteilungen bestimmte. Die Benutzer konnten auf einfache Weise verschiedene stochastische Funktionen für jeden dieser Parameter zuweisen und mit ihnen experimentieren.
Wie Xenakis‘ Glissandi-Generatoren enthielt auch Stochos mehrere Rampengeneratoren für jedes Ereignis, die auf stochastischen Berechnungen beruhten. Diese Rampengeneratoren konnten dann verschiedenen Syntheseoperationen zugewiesen werden, ähnlich wie eine Matrixmodulationsschnittstelle bei einem Synthesizer.

Ich begann mich jedoch schnell zu fragen, wie ich die Komplexität des generativen Modells erhöhen könnte, um eine klangliche Emergenz auf der Mikro-, Meso- und Makroebene (vertikale Organisation) zu erreichen und gleichzeitig Interdependenzen in der Progression zu etablieren. Inspiriert von natürlichen Prozessen bestand meine Lösung darin, die Selbstähnlichkeit innerhalb komplexer Strukturen anzuwenden und dabei einen Bottom-up-Ansatz zu verfolgen, der der evolutionären Entwicklung ähnelt. Ich habe dieses erweiterte Modell "Cosmosf" genannt, wobei das "f" für Feedback steht.
Das Modell Cosmosf
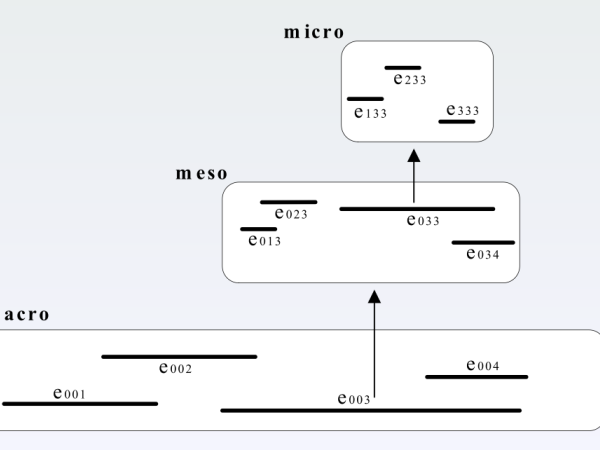
Figure 19. The Cosmosf model is a multi-scale and self-similar structure.
Das Modell Cosmosf beginnt mit der Eröffnung eines Zeitrahmens auf der Makroebene und füllt ihn mit Ereignissen, wie es Xenakis vorgeschlagen hat. In diesem Modell öffnet jedoch jedes Ereignis innerhalb des Makrorahmens einen neuen Raum auf der Mesoskala, und jedes Ereignis innerhalb des Mesorahmens öffnet einen weiteren Raum auf der Mikroebene (Abbildung 19). Dieser Ansatz führt Selbstähnlichkeit ein, erhöht die Komplexität in der vertikalen Organisation und schafft neue Wege für die Entstehung von Klängen, ähnlich wie in der Natur vorkommende Prozesse.
In Xenakis‘ Modell definieren die verteilten Ereignisse direkt die klanglichen Einheiten, während diese Definition im Cosmosf-Modell von den Mikro-Ereignissen übernommen wird. Die Meso-Ereignisse umfassen die Audiokomposition jedes Mikroraums, und die Makro-Ereignisse umfassen die Audiokomposition jedes Mesoraums, was zu einer Organisation von unten nach oben führt.
Hierarchische Struktur – Selbstähnlichkeit – Operationen auf mehreren Zeitskalen
Die Realisierung eines solchen Modells in Echtzeit-Audio-Software war dank der Einführung der JavaScript-Unterstützung in Max/MSP im Jahr 2005 möglich. In Abbildung 20 sehen Sie die Max/MSP-Version, die jedem Mikroereignis Audiosamples zuordnet.
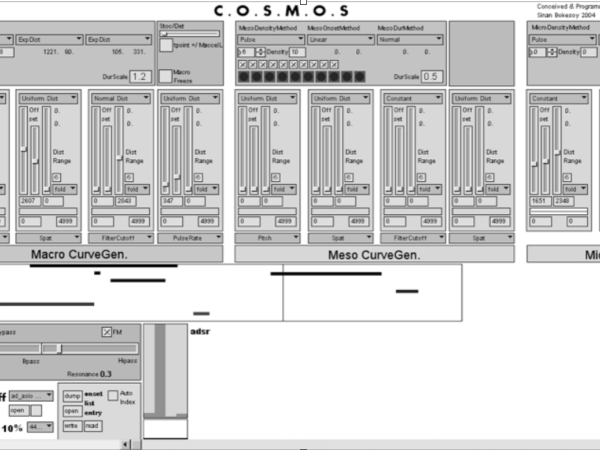
Figure 20. The Cosmosf model was realized first on MaxMSP in 2005 as a real-time event generator and synthesizer.
Im Jahr 2006 habe ich eine Rückkopplungsschleife von der Makroausgabe zurück zu den klanglichen Einheiten auf der Mikroebene innerhalb der Anwendung eingeführt. Das bedeutet, dass der nächste Makro-Zeitrahmen Spuren des Audioinhalts des vorherigen Makro-Ausgangs enthält, die dann in die Mikroebene des neuen Cosmosf-Zeitrahmens eingespeist werden (Abbildung 21).
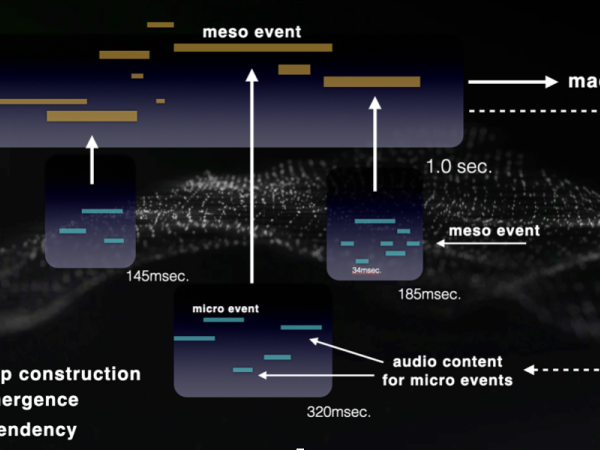
Figure 21. The bottom-up audio construction process with feedback.
In diesem Modell aktualisiert die Struktur kontinuierlich ihren klanglichen Inhalt auf der Grundlage des Outputs des vorherigen Frames. Die Erzeugung von Ereignissen erfolgt weiterhin von oben nach unten, während die Audiokonstruktion von unten nach oben erfolgt, und zwar über mehrere Zeitskalen hinweg, ähnlich wie emergente natürliche Prozesse. Die Mikroereignisse werden kontinuierlich von den Audiosignalen beeinflusst, die aus dem Output der Makroebene abgeleitet werden.
Da Xenakis keine Möglichkeit hatte, solche Signalverarbeitungsmechanismen zu implementieren, wurde die Ausgabe seiner Berechnungen direkt auf definierten akustischen Instrumenten abgebildet. Sein Ansatz beruhte auf Glissandi-Operationen, um die Spektraldichte zu formen, und nicht auf einer Bottom-up-Struktur. Es ist wichtig zu betonen, dass der Zweck dieser Anwendungen nicht allein darin besteht, Daten für die Zuordnung zu akustischen Instrumenten zu erzeugen. Vielmehr bieten sie die Möglichkeit, diese Ideen und generativen Modelle auf verschiedene Musikgenres anzuwenden.
Cosmosf Software-Entwicklung: Saturn, FX und M31
Ich würde sagen, dass die Entwicklung von Cosmosf im Jahr 2011 begann, nachdem ich auf eine C++-API umgestiegen war. Diese Umstellung überwand viele Einschränkungen und ermöglichte es mir, die CPU zugunsten der Audioqualität an ihre Grenzen zu bringen. Die C++-Version verfügte über OpenGL-Grafiken, ein spezielles, an Tron erinnerndes Oberflächendesign, Audioratenberechnungen für jede Modulationsquelle und viele kundenspezifische DSP-Implementierungen. (Abbildung 22)
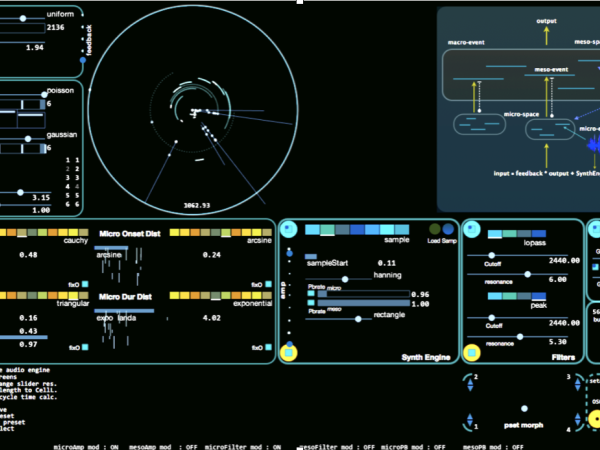
Figure 22. The first version of Cosmosf application was developed in C++.
Die grafischen Möglichkeiten moderner Computer und das Design für Datenvisualisierung und Interaktion sind Themen, die es wert sind, erforscht zu werden – etwas, das es zu Xenakis‘ Zeit noch nicht gab. Für Xenakis beschränkte sich die Datenvisualisierung weitgehend auf Partituren.
Ein einzigartiger Aspekt von Cosmosf (2011) ist die Visualisierung der mehrstufigen und hierarchischen Ereignisgenerierung. Im Gegensatz zum Modell der monoskaligen Ereignisgenerierung, das ein einfaches Zellengitter verwendet, stellt Cosmosf das Makroereignis als vollständigen Zyklus dar. Innerhalb dieses Zyklus symbolisieren Bögen Meso-Ereignisse, während Punkte Mikro-Ereignisse anzeigen. ( Abbildung 23 )a
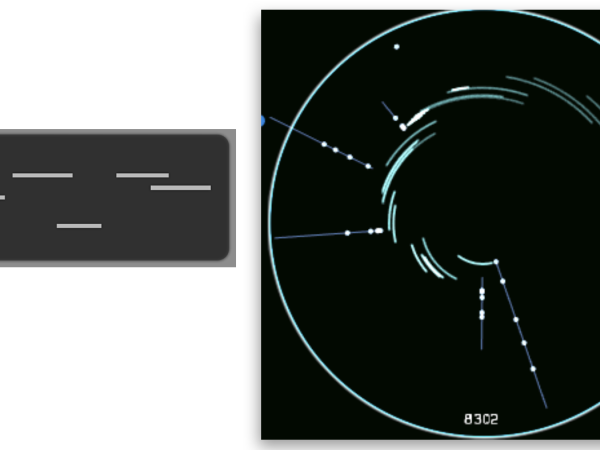
Figure 23. The visualization of multi-scale event distribution in Cosmosf.
Xenakis‘ berechnetes Glissandi-Modell wurde zunächst als LineGenerator in Stochos und später in Cosmosf implementiert. Der Startoffset und die Rampengeschwindigkeit derLinie können mit einer Reihe von stochastischen Verteilungen moduliert werden, die dem Benutzer zur Verfügung stehen.
Cosmosf enthält auch LFO-Generatoren (Low-Frequency Oscillator), die jeweils durch stochastische Funktionen moduliert werden können, um ihre Parameter Geschwindigkeit und Amplitude/Intensität zu variieren. Wie in Abbildung 24 dargestellt, ermöglicht dies die Erstellung komplexer Wellenformen, die als Modulationsquellen dienen.
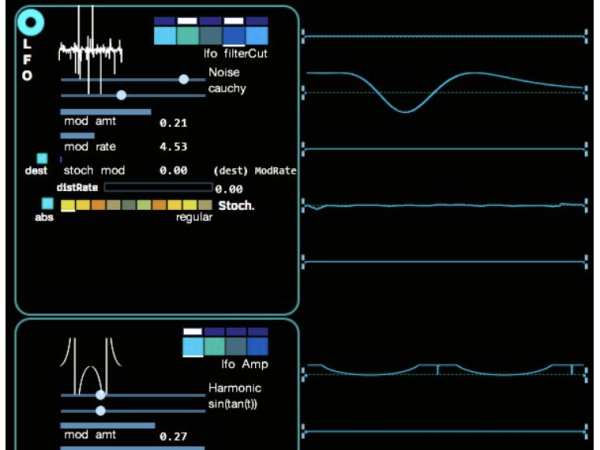
Figure 24. The stochastic LFO section on Cosmosf.
Jedes Mikro- und Meso-Event in Cosmosf ist mit mehreren LineGens und LFOs ausgestattet, die als Modulationsquellen dienen. Die Abbildung unten veranschaulicht die Komplexität, die die Anwendung durch ihre berechneten Daten erreichen kann. Sie können auch eine Liste der möglichen Modulationsziele für die LFO- und LineGEN-Modulatoren sehen. (Abbildung 25)

Figure 25. The modulation destinations of LFO’s and LineGen’s on Cosmosf.
Um Ihnen eine Vorstellung von der Rechenleistung von Cosmosf zu geben, hier ein paar Zahlen: Ein einzelnes Makro-Ereignis kann bis zu 11 Meso-Ereignisse haben, und jedes Meso-Ereignis kann bis zu 11 Mikro-Ereignisse enthalten. Jedes Meso-Ereignis umfasst 5 LineGens und 5 LFOs, während jedes Mikro-Ereignis aus 6 LineGens und 5 LFOs besteht. Diese Struktur zeigt die Fähigkeit der Anwendung , eine beträchtliche Menge an Daten und Modulationsquellen zu verarbeiten, und trägt zu ihren komplexen und dynamischen Klangerzeugungsfähigkeiten bei.
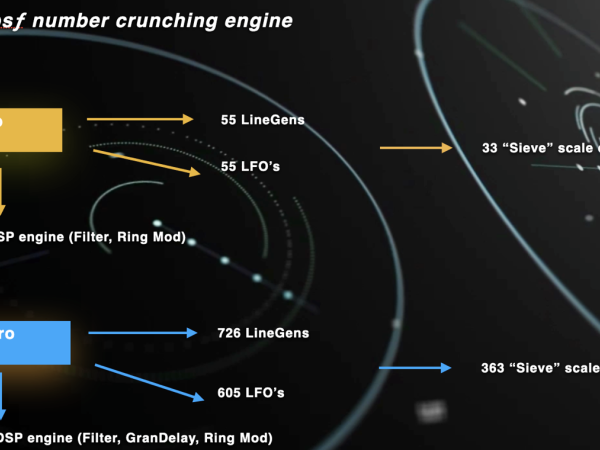
Figure 26. The calculation network in Cosmosf which increases in a fractal manner due to the multi-scale structure.
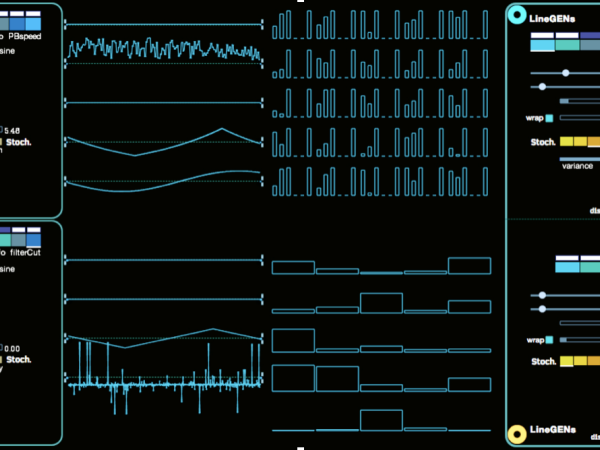
Figure 27. The modulation page projects all calculations in realtime.
Seit Cosmosf v3 umfasst das System zur Erzeugung von Ereignissen duale Makroereignisse und zwei Universen. Die dualen Makroereignisse können als para-phonisch betrachtet werden, während das Zwei-Universen-System wie Paralleluniversen funktioniert: Die Struktur bleibt identisch, aber die Ergebnisse unterscheiden sich, weil die Iterationen der stochastischen Funktionen zu unterschiedlichen Zuständen führen. Abbildung 28 zeigt die systemische Organisation der beiden Universen.
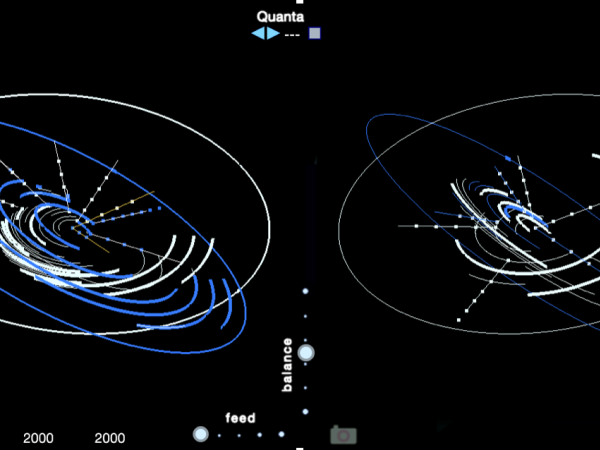
Figure 28. The dual universe and dual macro-event Cosmosf.
Von einem Universum kann der Ausgang des Makroklangs in das zweite Universum eingespeist werden. Dies sind Inspirationen von kosmologischen Konzepten, die auf das Cosmosf-Modell angewendet werden.
Operationen mit den berechneten Ereigniswerten (Beginn, Dauer)
Verschiedene Operationen können die lokale Dichte, das Gleichgewicht zwischen totaler Zufälligkeit und Musterschleifen, die rhythmische Quantisierung und die zeitliche Kompression oder Expansion beeinflussen. Der linke Teil der Anwendungsschnittstelle ist diesen Operationen im Zeitbereich gewidmet und kann in Echtzeit aufgerufen werden. ( Abbildung 29 )
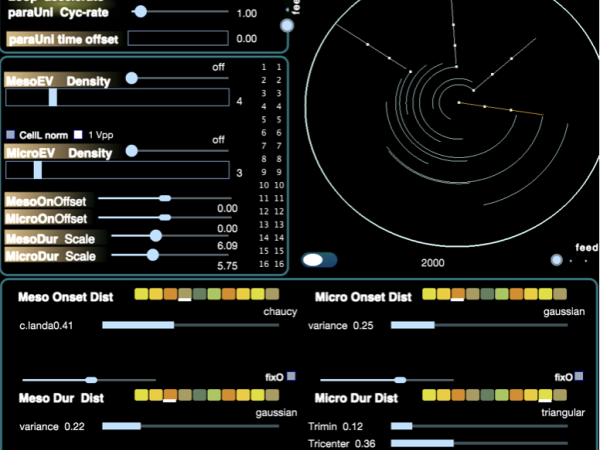
Figure 29. The event distribution parameters are concentrated on the left part.
- Die Ergebnisse der stochastischen Verteilungen in Cosmosf können quantisiert werden. Ähnlich wie bei einem normalen DAW-Sequenzer können die Werte für Beginn und Dauer jedes Mikro- und Meso-Ereignisses an klassischen Notenlängen wie 4, 8, 16 und 32 sowie an Triolenwerten ausgerichtet werden. Dadurch kann das Cosmosf-Event-Generierungssystem wie eine Variation eines euklidischen Sequenzers funktionieren und komplexe polyrhythmische Strukturen erzeugen.
- Wir können die Dauer von Meso- oder Mikroereignissen um einen bestimmten Wert skalieren, wodurch Überschneidungen entstehen und sich die lokale Dichte ändert.
- Durch ständiges Schrumpfen oder Ausdehnen der Bögen zum Ursprung des Cosmosf-Kreises hin oder von ihm weg erreichen wir eine Kompression oder Expansion der Zeit.
- Außerdem können wir die Verteilungen für Meso- oder Mikroereignisse einfrieren, so dass die zuletzt berechneten Werte für Beginn und Dauer unverändert bleiben, was zu einem Schleifenmuster auf dieser Skala führt.
Siebe
Cosmosf stellt eine der frühesten Anwendungen von Tonhöhenquantisierern vor, die die von den Modulatoren berechneten Rohwerte auf die ausgewählten musikalischen Skalen oder Divisionen quantisieren. In Cosmosf können nicht nur die Tonhöhe, sondern auch andere Syntheseparameter auf der Meso- oder Mikro-Ebene quantisiert werden.
Um diesen Prozess zu visualisieren, habe ich das Frequenzspektrum mit dem Farbspektrum verknüpft und ihre jeweiligen Wellenlängen aufeinander abgestimmt. Dadurch entsteht eine faszinierende Korrelation zwischen den hörbaren Wellenlängen von Schallwellen und den sichtbaren Wellenlängen von Lichtwellen. Der obere Teil zeigt die Rohwerte als durchgehende Linie des Farbspektrums, während der untere Teil die quantisierten Zustände als einzelne Punkte darstellt. ( Abbildung 30 )
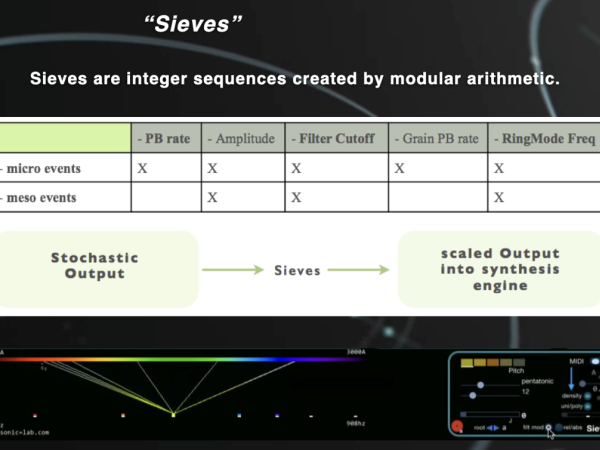
Figure 30. The Sieves interface represents sound frequencies with color wavelengths.
Morphing
Ein klanglicher Morphing-Prozess ist eine Metapher für die Erforschung der klanglichen Form und der klanglichen Entwicklung auf Zwischenebenen zwischen zwei oder mehr klanglichen Materialien. Es gibt keine robuste Methodik, um exakte Lösungen für Morphing-Prozesse zu finden, aber sie bieten ein reiches Terrain an Möglichkeiten, die in verschiedenen Ansätzen behandelt werden können, um interessante Wahrnehmungsphänomene zu erzeugen.
Sound-Morphing kann durch Überblendung der Parameter der konsistenten Strukturen erfolgen, die die Quell- und Zielsounds erzeugen. Eine Instanz des Morphing-Prozesses weist auf einen bestimmten Zustand zwischen zwei oder mehr Klängen/Preset-Parametern hin, der als mehrdimensionaler Vektor im Parameterraum dargestellt werden kann.
In unserem Fall ist diese quantifizierbare und kontrollierbare Klangeinheit diejenige, die über die Benutzeroberfläche / alle voreingestellten Parameter definiert wird, die das Cosmosf-System definieren, das den Klang erzeugt. Daher stellt jede Voreinstellung einen Vektorzustand dar, der auf eine Menge von Parametern verweist.
Der Morphing-Prozess in Cosmosf platziert vier verschiedene Voreinstellungen an den Ecken eines Tetraeders, der die Oberfläche einer umgebenden Kugel berührt. Der Morphing-Zeiger stellt einen beliebigen Punkt innerhalb dieser Kugel dar, und der euklidische Abstand von diesem Punkt zu jeder Voreinstellung bestimmt das Gewicht dieser Voreinstellung im resultierenden Parameterzustand. (Abbildung 31)
Der Morphing-Zeiger kann manuell durch Angabe von Polarkoordinaten innerhalb der Kugel, mit Hilfe mathematischer parametrischer Funktionen (wie in der Abbildung links dargestellt) oder durch kontrollierte stochastische Funktionen, die die Polarkoordinaten (Winkel und Radius) anpassen, bewegt werden.Oder:
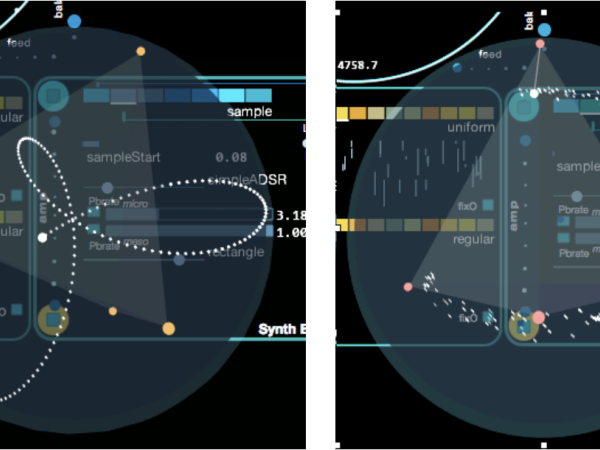
Figure 31. The Morphing pointer can be manipulated in various waves.
Die 2013 eingeführte Cosmosf-Morphing-Engine war einzigartig in ihrer Fähigkeit, den Morphing-Prozess mit einer Audio-Rate durchzuführen. Das bedeutet, dass nicht nur die einzelnen Morph-Zustände, sondern auch das Verhalten des Morphing-Pointers bei der Bewegung von Punkt A zu Punkt B die Spektralmorphologie des resultierenden Klangs maßgeblich beeinflusst.
3D-Klangverräumlichung in Cosmosf
Ich habe mehreren wichtigen Aufführungen von Xenakis‘ Stücken beigewohnt, und einer der beeindruckendsten Aspekte, die man live miterleben kann, mit vollem Blick auf die gesamte Szene (etwas, das in Aufnahmen, die auf YouTube verfügbar sind, oft verloren geht), ist das Zusammenspiel zwischen den Bewegungen der Darsteller ements, Klang und Raum. In stochastischen und chaotischen Prozessen veranschaulichen die sich wiederholenden Reaktionen von Individuen in der Bewegung einer Menschenmenge oder im Schwarmverhalten anschaulich den emergenten Charakter des Systems, in dem individuelle Aktionen zur kollektiven Dynamik beitragen. Xenakis macht sich diese räumliche Verteilung von Ereignissen zunutze und macht sie in Orchesteraufführungen sichtbar.
Ein System zur Erzeugung von Ereignissen wie Cosmosf sollte in der Lage sein, diese Bewegung durch Klangverräumlichung zu vermitteln. Heute sind wir in der Lage, das Quellensignal im Ambisonic-Format zu kodieren, so dass jeder Lautsprecher in einem Projektionssystem zur präzisen Lokalisierung der Klangquelle im Aufführungsraum beitragen kann.
Mit der späten Version von Cosmosf aus dem Jahr 2015 wurde die Möglichkeit eingeführt, Sound in einem Ambisonic-Format dritter Ordnung zu rendern und als entsprechende Mehrkanal-Audiodatei zu exportieren, die später dekodiert werden kann. Die Surround-Sound-Engine handhabt dies, indem sie Signale auf der Meso-Ebene nimmt und, ähnlich wie die 3D-Sphäre, die in der Morphing-Engine verwendet wird, ihre Positionen innerhalb dieser Sphäre verteilt. Jedes Meso-Ereignis kann deterministisch lokalisiert, mit einer parametrischen Funktion entlang einer Kurve bewegt oder mit kontrollierten stochastischen Funktionen positioniert werden. (Abbildung 32)
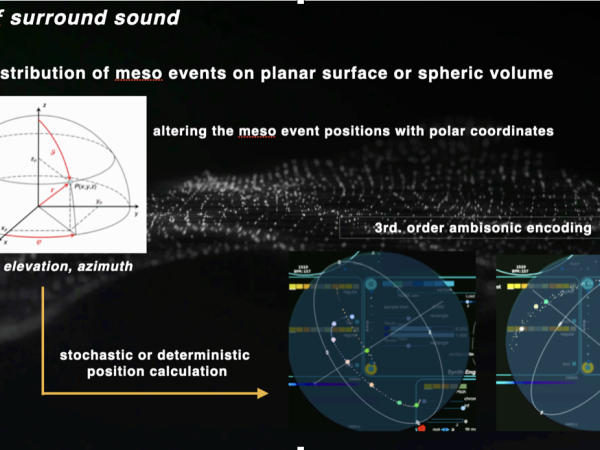
Figure 32. The sound spatialization process on meso events.
Bei diesem Ansatz können die Ereignisse durch die Begrenzung der Parameter Radius und Polarwinkel auf bestimmte Abschnitte des räumlichen Feldes verteilt werden.
Die Verfügbarkeit von Cosmosf
Cosmosf bietet viele zusätzliche Funktionen, aber es ist unnötig, hier auf alle Einzelheiten einzugehen. Ich habe die bemerkenswertesten innovativen Aspekte hervorgehoben und wie Cosmosf von Xenakis‘ Modellen abweicht. Derzeit gibt es drei Versionen, die von www.sonic-lab.com vertrieben werden: Cosmosf Saturn, Cosmosf FX und Cosmosf M31. Alle kommen im Plugin-Format und laufen in einer DAW.
Cosmosf Saturn ist ein Synthesizer, der Mikro-Event-Audioinhalte mit Hilfe von zugewiesenen Synthesetechniken erzeugt, die von der Wiedergabe von Sample-Dateien bis hin zur grundlegenden physikalischen Modellierung reichen.
Cosmosf FX ist ein Live-Audioprozessor, der sich auf die Live-Audioverarbeitungsfähigkeiten der Cosmosf-Synth-Engine konzentriert. Strukturell sind Cosmosf Saturn und Cosmosf FX identisch.
Cosmosf M31 ist ein MIDI-Event-Generator, der MIDI-Noten-Events für die Mikro- und Meso-Events von Cosmosf erzeugt. Diese Ereignisse umfassen mehrere LFOs und LineGens, die in kontinuierliche MIDI-Controller-Befehle übersetzt werden. ( Abbildung 33)

Figure 33. Cosmosf M31 and MBots running on a DAW.
Cosmosf M31 enthält auch ein Bot-Plugin, das auf jeder anderen DAW-Spur platziert werden kann und die Kommunikation zwischen Plugins ermöglicht, um Informationen auszutauschen. M31 fungiert als Dirigent eines Orchesters, während die MBots als einzelne Mitglieder zusammenarbeiten und ihre Aktionen in Echtzeit koordinieren.
Die Entwicklung dieser drei Anwendungen erstreckte sich über mehr als ein Jahrzehnt, und sie sind nach wie vor mit den modernen Produktionsanforderungen und -umgebungen von heute kompatibel.
Es gibt zahlreiche Videos zu Cosmosf Saturn und FX auf YouTube. Auch der Cosmosf M31 hat eine eigene Playlist.
Zum Abschluss des 1. Teils meiner Übersicht über generative Audiomodelle
Generative Audiosynthese und Musik bieten nach wie vor grenzenlose Möglichkeiten zur Erforschung, Innovation und Entwicklung. Um ihr Potenzial voll auszuschöpfen, ist es unerlässlich, alte Praktiken mit neuen technologischen Werkzeugen zu überdenken und neu zu interpretieren und sich intensiv mit diesen Prozessen auseinanderzusetzen, um ihre verborgenen Dimensionen aufzudecken. Im Kern definiert sich die generative Audiosynthese nicht nur durch die Komplexität ihrer Modelle, Algorithmen oder künstlichen Intelligenz, sondern durch die Tiefe, mit der diese Modelle wichtige Sounddesign-Konzepte interpretieren, abbilden und weiterentwickeln können,. B. die Entwicklung von Klangfarben, klangliche Interaktion und strukturelle Feinheiten. Ihr wahres Wesen liegt in ihrer Fähigkeit, die grundlegenden Prinzipien der Klangkomposition zu erfassen und auszudrücken, sei es durch einfache oder komplizierte Systeme, und die einzigartige Vision und Absicht ihres Schöpfers widerzuspiegeln.
In diesem Überblick habe ich die historischen Grundlagen und zentralen Ideen hinter generativen Modellen hervorgehoben und untersucht, wie sie die Komposition von Klängen sowohl vertikal als auch horizontal gestalten und wie sie sich durch aleatorische Methoden von natürlichen Prozessen inspirieren lassen. Ich habe mich auch auf die Pionierarbeit von Iannis Xenakis konzentriert, der ein Leben lang mathematische Modelle auf Musik anwandte, traditionelle Vorstellungen von Komposition in Frage stellte und neue Möglichkeiten eröffnete.
Heute geht eine Audioanwendung weit über die Grenzen eines bloßen Modells hinaus; sie umfasst eine multidisziplinäre Verschmelzung von mathematischer Theorie, wissenschaftlichem Verständnis, Klangkunst, visuellem Design und Produktentwicklung. Mein Weg, von meinen frühen akademischen Studien zu Xenakis‘ Werk bis zu den aktuellen Iterationen meiner Cosmosf-Anwendungen, spiegelt mehr als 20 Jahre engagierter Entwicklung und praktischer Anwendung wider, ist aber immer noch ein unfertiges Werk.
Generative Audio ist nicht nur ein Werkzeug für die Komposition, sondern spiegelt auch den Wunsch des Menschen wider, die dynamischen, emergenten Eigenschaften des Universums selbst zu verstehen, zu erforschen und neu zu erschaffen. Dieser Ansatz lädt uns dazu ein, Musik nicht nur als ein handwerklich hergestelltes Objekt zu betrachten, sondern als einen lebendigen Prozess, der sowohl von den Algorithmen, die ihn antreiben, als auch von den kreativen Köpfen, die mit diesen Werkzeugen arbeiten, kontinuierlich geformt wird. In Zukunft wird sich dieser Dialog zwischen Technologie, Kunst und Natur weiter ausweiten und neue Möglichkeiten bieten, sich mit Klang auseinanderzusetzen und die Grenzen der Musik selbst neu zu definieren.
Die Reise geht weiter, geleitet von Neugierde, Innovation und einem unermüdlichen Streben nach neuen Möglichkeiten.
Sinan Bökesoy
Sinan Bökesoy ist Komponist, Klangkünstler und Hauptentwickler von sonicLAB und sonicPlanet. Bökesoy, der an der Universität Paris8 unter der Leitung von Horacio Vaggione in Computermusik promoviert hat, hat sich eine Nische in der Synthese von sich selbst entwickelnden Klangstrukturen geschaffen. Inspiriert von Komponistengrößen wie Xenakis, nutzt er in seiner Arbeit algorithmische Ansätze, mathematische Modelle und physikalische Prozesse, um innovative Audiosyntheseergebnisse zu erzeugen. Bökesoy strebt einen ausgewogenen Arbeitsablauf an, der Theorie und Praxis sowie künstlerische und wissenschaftliche Ansätze miteinander verbindet. Bökesoy hat seine Arbeit bei renommierten Veranstaltungen wie Ars Electronica / Starts Prize, IRCAM, Radio France Festival, internationalen Biennalen und Kunstgalerien vorgestellt. Er hat mehrfach auf Konferenzen wie ICMC, NIME, JIM und SMC sowie im Computer Music Journal, MIT Press, veröffentlicht und präsentiert.
Artikelthemen
Artikelübersetzungen erfolgen maschinell und redigiert.
 Sinan Bökesoy
Sinan Bökesoy