Beyond Digital Beats: Quantum Computers and the Future of Music

News that a mad scientist or a ruthless IT company built yet another gadget that can create music is like a broken record these days. Honestly, there is nothing extraordinary here. The truth is that AI has been making music since the 1950s. Seventy years later, Frankensteinian robots have not replaced musicians. We are still around. Possibly more so than ever.

Nevertheless, I have a hunch that music technology is on the verge of a significant leap within the next decade. But not single-handedly by AI. Rather, I am thinking of new kinds of computing hardware, in particular, quantum computers.

Quantum computers are like a supercharged version of digital computers. The latter processes information encoded as bits, which are like tiny electronic switches that can be either 0 or 1. Digital computers process data in a linear, step-by-step manner.  Conversely, quantum computers use quantum bits or qubits. These qubits can process 0 and 1 at the same time, thanks to a quantum mechanical phenomenon called superposition. Thus, quantum computers can explore many possibilities simultaneously. This allows them to handle a vast amount of information and perform complex calculations faster than digital computers.

In simpler terms, a classical digital computer works like someone solving a maze one step at a time. In contrast, a quantum computer can explore all possible paths at once and work out an exit route much faster. But speed is not the only potential advantage. Operating a quantum computer requires different ways of thinking about encoding and processing information. And this is where composers might benefit big time. This new technology is bound to enable us to develop new ways to create new music, new styles, and new modes of delivery.

The small print is that quantum computers are still in development. A handful of machines have been built and a few companies already provide access to rudimentary quantum hardware on the cloud for research. But they are not widely available. And, indeed, they are expensive. Very expensive. We are talking here about several millions of Euros. To put this in perspective, a decent personal computer today costs a mere few hundred Euros.

It is often said that the stage of development of quantum computers today is comparable to the stage of development of the large computer mainframes of the 1950s. But the industry is making terrific progress and a few opportunities for giving musicians access to this technology are emerging. As we speak, composers already are taking quantum computing programming courses and residencies in research laboratories to explore this new technology. For instance, the Yale Quantum Institute in the USA has run an artist-in-residence scheme since 2017. Each year the institute welcomes a visual artist or a musician for a year-long residency to produce a quantum science-based piece. And the Goethe Institute in Germany has recently launched an international artist-in-residence programme called Studio Quantum.

It looks as though history is repeating itself. Back in the 1950s, when computers were nonetheless dodgy to use, expensive, and not widely available, composers started frequenting research laboratories to experiment with them. Over the last 70 years or so, progress in computing technology and the music industry has gone hand in hand. Computers have played a pivotal part in the development of today’s burgeoning music industry. Importantly, composers interested in exploring the potential of computing technology for their métier played a significant role in these developments.

For instance, in the early 1950s, Australia’s Council for Scientific and Industrial Research (CSIR) installed a loudspeaker on their Mk1 computer to track the progress of a program using sound. Subsequently, Geoff Hill, a mathematician with a musical background, programmed this machine to playback folk tunes.

But the first significant milestone of computer music took place in 1957 at the University of Illinois at Urbana-Champaign, USA, with the composition lliac Suite by Lejaren Hiller and Leonard Isaacson. Hiller, then a professor of chemistry, collaborated with mathematician Isaacson to program the ILLIAC machine to compose a string quartet.

The ILLIAC, short for Illinois Automatic Computer, was one of the first mainframe computers built in the USA, comprising thousands of vacuum tubes. They programmed this machine with rules of harmony and counterpoint. The output was transcribed manually into a musical score for a string quartet. Whereas Mk1 merely played back an encoded tune – like a pianola – ILLIAC was programmed with algorithms to compose music. Hence Illiac Suite is often cited as a pioneering piece of computer-generated music.

Various developments have taken place since, notably the invention of the transistor and subsequently the microchip. The microchip enabled the manufacturing of computers that became progressively more accessible to a wider sector of the population.

Another significant milestone took place in the early 1980s at IRCAM with the composition of Répons. This is an unprecedented composition by the celebrated French conductor Pierre Boulez. IRCAM (short for Institut de Recherche et Coordination Acoustique/Musique) is a centre for research into music and technology founded in 1977 in France by Boulez himself.

Répons, for chamber orchestra and six solo percussionists, was the first significant piece of classical music to use digital computing technology to perform live on stage. The machine "listened" to the soloists and responded with synthesised sounds on the spot during a performance. To achieve this, Boulez used the 4X System developed at IRCAM by physicist Giuseppe Di Giugno and his team. 

If you ask me, Répons epitomises the beginning of an era of increasingly widespread use of digital computers to develop new approaches to composition and performance. It signifies the beginning of our present time, where personal computers, laptops, notebooks, tablets, and even smartphones are used in musical composition and performance.

Quantum computing has been on my radar since the turn of the century. In the beginning, it was all theoretical, weird, and awkward to grasp. There were no actual quantum computers built at the time. It was only in 2017 that I found out that Rigetti Computing, then a start-up firm based in Berkeley, California, announced that they had built a quantum computer and were looking for beta testers to have a go with it. In no time, I packed my suitcase and scooted to Berkeley to see it all for myself. The rest is history.

I completed Zeno, my first fully-fledged composition using quantum computers in 2018. Zeno is an exploratory piece for bass clarinet and electronic sounds. During the performance, a local laptop listened to tunes played on the clarinet and extracted compositional rules. These rules were converted into quantum algorithms and transmitted to the quantum computer in California through the Internet. Then, the quantum machine ran the algorithms and relayed the results to my laptop, which was rendered into synthesized musical responses. The quantum computer acted as a buddy musician who improvised with the clarinet tunes, as if in a jazz-like gig. Video 1 shows a recording of Zeno made at the University of Plymouth, UK, with Sarah Watt on the bass clarinet. Omar Costa Hamido and I operated the electronic sounds and the Rigetti machine on the cloud, respectively.

Zeno is a milestone for me. What I have achieved with a rudimentary quantum computer sporting only a few qubits would require sophisticated AI programming for a state-of-the-art desktop digital machine. This reinforced my hunch that music technology is on the verge of a significant leap. The thought of what fully fledged quantum computers might afford musicians in 20 or even 10 years is mind-boggling. 

But what is quantum computing? How can a quantum algorithm represent musical rules? How can the results of processing a quantum algorithm make music? First, let us examine in more detail what makes a quantum computer different from a digital one.

I mentioned earlier that a quantum computer deals with information encoded as quantum bits or qubits. The qubit is to a quantum computer what a bit is to a digital one: it is a basic unit of information. In hardware, qubits live in the subatomic world. They are subject to the laws of quantum mechanics. This makes qubits process information fundamentally differently from how digital bits do it.

To picture a qubit, imagine a transparent sphere with opposite poles denoted by |0⟩ and |1⟩, which is the convention used to represent quantum states. From its centre, a vector whose length is equal to the radius of the sphere can point to anywhere on the surface. In quantum mechanics, this sphere is called the Bloch sphere, and the vector is referred to as a state vector. The state vector of a qubit represents a quantum state and can be described in terms of polar coordinates using two angles, θ and φ, as shown in Figure 1.

© Smite-Meister, licensed under CC BY-SA 3.0

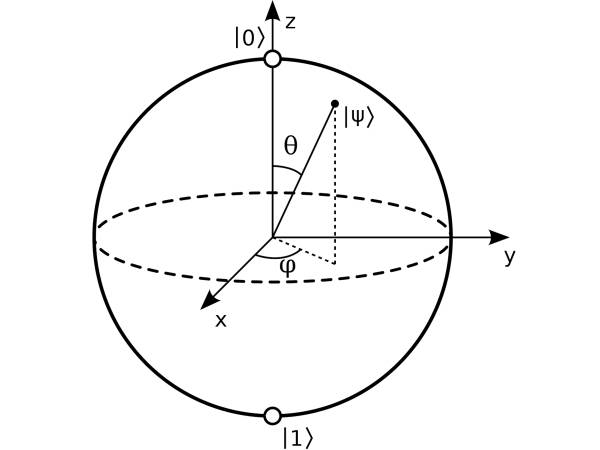
Figure 1: The Bloch sphere is a geometric representation of a qubit.

A state vector can point anywhere between the north and south poles of the Bloch sphere. When it does so, the qubit is in a state of superposition between |0⟩ and |1⟩. In short, the qubit can represent both simultaneously. But the qubit will always value 0 or 1 when we read it.

In a state of superposition, the state vector is normally described as a linear combination of |0⟩ and |1⟩. For instance, state vector |Ψ⟩ is notated as |Ψ⟩= α|0⟩+ β|1⟩, where the coefficients α and β represent tendencies towards the north or the south, respectively. In simpler terms, the position of the vector on the Bloch sphere indicates whether the qubit is more likely to value 0 (when pointing to a region above the equator line) or 1 (when pointing below the equator line) when it is read out. In quantum computing terminology, α and β are referred to as amplitudes and the act of reading a qubit is referred to as "measuring".

The weirdest thing in all this is that quantum computers process information with qubits in superposition. A good part of the art of programming a quantum computer involves manipulating qubits while in such an indeterminate state.

Quantum computers are programmed by applying sequences of operations to qubits. In quantum computing terminology, qubit operations are called gates. Quantum computing programming tools provide several gates.

RX(𝜋) gate rotates the state vector of a qubit by 180 degrees around the x-axis of the Bloch sphere geometry. Thus, if the qubit vector is pointing to |0⟩, then this gate flips it to |1⟩ and vice-versa. The RX(𝜋) gate is often referred to as the NOT gate and notated as X. A program is often depicted as a circuit with quantum gates operating on qubits. Hence, a program is called a quantum circuit in quantum computing terninology.

Performing operations on groups of qubits in superposition enables manipulations on many possible configurations of information simultaneously. Putting this into perspective, a digital processor deals with information represented by a series of bits switched on and off individually. For instance, with 3 bits, a system can represent numbers 0 to 7 as follows: 000, 001, 010, 011, 100, 101, 110, and 111, respectively. A digital processor deals with this data one at a time. With 3 qubits, however, a quantum processor represents those numbers simultaneously for processing them in parallel.

With 20 qubits, a system would simultaneously handle over one million pieces of information represented as quantum states in superposition. Currently, some quantum computers already have hundreds of qubits. This is not a big deal yet. But it is expected they will have thousands or millions of qubits soon. There are several issues to be solved before these machines can leverage large amounts of qubits for computation. But this is not a question of if, but when.

The wonders of quantum computation do not end here. In addition to superposition, quantum programming involves entangling groups of qubits. Entangled qubits interact – or interfere – with one another and are no longer considered individually. They create a quantum system of their own. To unpack this, let us contemplate how the abstract notion of qubits relates to the physical world.

Consider the case of an electron. In quantum mechanics, the physical state of an electron is unknown until one observes it. Before it is observed, the electron is said to behave like a wave. When it is observed, it becomes a particle. This phenomenon is referred to as the wave-particle duality. Qubits are exquisite because they embody this duality.

Quantum systems can be described in terms of wave functions. A wave function depicts a quantum system as the sum of the possible states that it may fall into when it is measured. In other words, it defines what a particle might be like when the wave is observed.

In quantum computing, the higher the number of qubits used to construct a wave function, the higher the number of possible outcomes a system may yield. Each possible component of a wave function is also a wave. They are scaled by amplitude coefficients reflecting their relative weights. Some states are more likely than others. Metaphorically, think of a quantum system as the spectrum of a musical sound, where the different amplitudes of its various wave components give its unique timbre.

As with sound waves, quantum wave components interfere with one another, constructively and destructively. In quantum physics, the interfering waves in a wave function are said to be coherent. The act of observing the wave function decoheres the waves. Again metaphorically, it is as if when listening to a musical sound one would perceive only a single spectral component; probably the one with the highest energy, but not always so.

Superposition, entanglement, and interference are key properties of quantum computing, which renders it fundamentally different from digital computing. An important characteristic of quantum computers is that the results of reading out quantum states cannot be predicted with absolute certainty. There are methods to get around this. However, it is not uncommon to leverage quantum unpredictability for specific applications, including music. Indeed, many composers have embraced stochasticity, from Mozart in the 18th century and Stockhausen in the 20th century, to almost anyone working with AI music models today.

Now, let us examine in more detail a method for making music interactively with quantum computers. I originally developed it for the composition Zeno, mentioned above. But I have been further developing and refining it since then. The latest incarnation was put into practice to compose Qubism. This is a sonata-like piece in three movements for a chamber group, quantum computer, and electronics, composed for the London Sinfonietta. 

The system extracts sequencing rules from input music and represents them in terms of quantum circuits. Then, it runs those quantum circuits to generate musical responses (Figure 2). Once the system has learned some rules, it can generate as many new tunes, of virtually any length, as required. 

© Eduardo R. Miranda

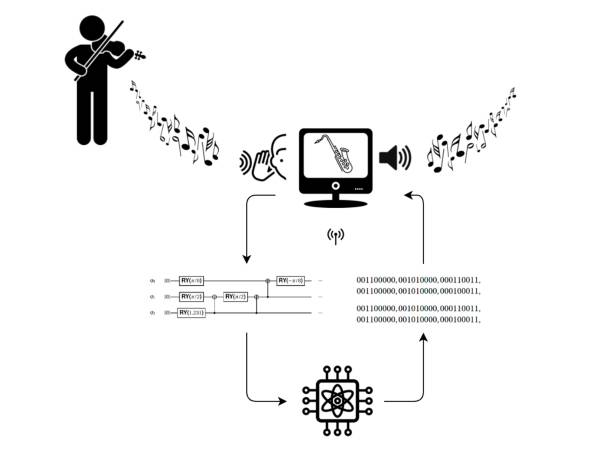
Figure 2: The quantum system developed for Qubism listens to a violin and produces responses during a performance.

Let us examine what the rules extracted by the system look like. Consider the system extracted the following rules from a hypothetical input tune:

C₃ => D₃(25%) V G#₃(25%) V C₄(25%) V D₄(25%)
D₃ => C₃(30%) V E₃(70%)
E₃ => D₃(25%) V F#₃(25%) V A#₃(25%) V C₄(5%) V D₄(20%)
F#₃ => E₃(100%)
G#₃ => C₃(30%) V A#₃(70%)
A#₃ => E₃(33%) V G#₃(33%) V C₄(34%)
C₄ => C₃(30%) V A#₃(70%)
D₄ => C₃(20%) V E₃(80%)

For instance, the second rule states that there is a 30% chance that a note 𝐷3 would be followed by note 𝐶3 and a 70% chance that it would be followed by note 𝐸3. The symbol “∨” stands for “or” and the percentage figure in parenthesis next to the notes is their weight coefficient, expressed here in terms of probability of occurrence. Thus, if we prompt the system with one of the above initial notes on the left side of the arrow, then it will process the respective rule and produce a new note. This new note is subsequently used to pick a rule to generate another note, and so on.

The quantum circuit for the second rule is depicted in Figure 3. This circuit sets up three qubits to produce a quantum state representing the probability distribution of the rule. To enable this, the system represents each distinct note with a binary code.

The larger the number of different notes in the input music, the higher the number of digits required to encode them. In the present example, the hypothetical input had eight notes. Thus, three digits are sufficient here. For instance, 𝐶3 = 000, 𝐷3 = 001, 𝐸3 = 010, and so on.

Therefore, in terms of the binary representation, the second rule is expressed as follows:

001 ⇒ 000(30%) ∨ 010(70%)

In this case, the respective circuit in Figure 3 programs the qubits in such a way that they would most likely produce either 000 or 010 when they are measured.

© Eduardo R. Miranda

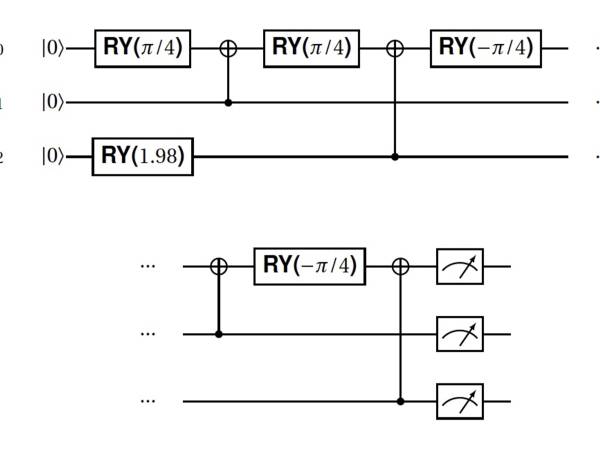
Figure 3: Circuit for the rule 100 ⇒ 000(30%) ∨ 101(70%).

The circuit is read from the left to the right. The various gates RY tell the system how to rotate the qubits 𝑞0, 𝑞1 and 𝑞2 along the meridian axis of the Bloch sphere. Upon measurement (represented by the boxes with a dial, at the end), the circuit should ideally output either 000 with a 30% probability or 101 with a 70%. (The qubits are read in this order: 𝑞2𝑞1𝑞0.)

There are moments on the score of Qubism indicating when the system listens to an instrument and generates a response. The current version of the system can listen to only one of the instruments of the ensemble: the violin.

Figure 4 shows an excerpt from the score illustrating a passage where the quantum computer listens to a tune played by the violin and produces a response lasting for circa 20 seconds.

© Eduardo R. Miranda

Figure 4: An excerpt from the score for Qubism.

The chamber group comprises a flute, trombone, marimba, violin, viola, and violoncello. The system generates responses using a synthesised saxophone and percussive sounds. The piece also has an electronically generated track (not shown in Figure 4), which I also composed with quantum computing using a method called Partitioned Quantum Cellular Automata, or PQCA. The PQCA method is explained in the book Quantum Computer Music: Foundations, Methods and Advanced Concepts, published by Springer in 2022.

I used an IBM Quantum machine on the cloud for the premiere of Qubism by London Sinfonietta at King’s Place, London, in June 2023. Video 2 shows an excerpt of the premiere. Watch for the section towards the end, where the violinist plays a solo tune, and the quantum computer generates responses with percussive sounds.

The example above is only a glimpse of how quantum computing can be harnessed for music. There is a growing community of musicians and quantum computing developers embracing this technology. They are developing innovative approaches to music making. Several of these were presented at the 2^nd International Symposium on Quantum Computing for Musical Creativity, which took place in Berlin in October 2023.  Quantum computers are right around the corner. 

The integration of quantum computing into the realm of music presents an exciting frontier that promises to revolutionize how we create, compose, and experience music. From accelerating the pace of musical innovation to unlocking new avenues of creativity, the potential of quantum computing in music knows no bounds. We do not know for sure how it will impact music. But we will not know until we try it.

As we continue to witness the convergence of technology and artistry, embracing the transformative potential of quantum computing in music promises to herald a new era for the music industry.